题目内容
(2012•衢州二模)在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点, 连接AB并延长AB至点D,使DB=AB,连接OB、DC相交于E,过E作OA的垂线,垂足为F,连接AE.
连接AB并延长AB至点D,使DB=AB,连接OB、DC相交于E,过E作OA的垂线,垂足为F,连接AE.
(1)如图,当∠AOB=15°时,①求弧AB的长; ②求△OAB的面积;
(2)在点B运动过程中,
①若以点E、C、F为顶点的三角形与△AOB相似,请求出此时点F的坐标;
②若以点E、C、F为顶点的三角形与△ABE相似,请直接写出此时点F的坐标.
 连接AB并延长AB至点D,使DB=AB,连接OB、DC相交于E,过E作OA的垂线,垂足为F,连接AE.
连接AB并延长AB至点D,使DB=AB,连接OB、DC相交于E,过E作OA的垂线,垂足为F,连接AE.(1)如图,当∠AOB=15°时,①求弧AB的长; ②求△OAB的面积;
(2)在点B运动过程中,
①若以点E、C、F为顶点的三角形与△AOB相似,请求出此时点F的坐标;
②若以点E、C、F为顶点的三角形与△ABE相似,请直接写出此时点F的坐标.
分析:(1)①如图,连接BC,根据圆周角定理得∠ACB=2∠AOB=30°,然后根据弧长公式计算弧AB的长;
②作BP⊥OA于P,根据圆周角定理得∠OBA=90°,根据含30度的直角三角形三边的关系得到BP=
,然后根据三角形面积公式求解;
(2)连结OD,由AB=BD,AB⊥OB,根据等腰三角形的判定方法得到△ODA为等腰三角形,则CB=
OD,CB∥OD,根据相似三角形的判定得△BCE∽△ODE,利用相似比得BE:OE=CE:DE=1:2,
①当Rt△ECF∽Rt△AOB时有∠AOB=∠ECF,则EO=EC,所以OF=
OC=
,得到F点坐标为(
,0);当Rt△ECF∽Rt△OAB,作DH⊥OA,易得∠BAO=∠FCE,则DC=DA,得到CH=
,利用EF∥DH得到CF:CH=CE:CD=1:3,可计算出CF=
,所以OF=
,于是得到F点坐标为(
,0);
②当Rt△ECF∽Rt△AEB,连结BF,由∠EFA=∠EBA=90°得到点E、F、A、B共圆,根据圆周角定理得∠AEB=∠AFB,而∠AFB=∠ECF,所以CE∥BF,则OC:OF=OE:OB=2:3,可计算出OF=
,得到F点坐标为(
,0);当Rt△ECF∽Rt△EAB时有∠ECF=∠EAB,又由∠EBA=90°,AB=DB可判断△EAD为等腰三角形,得∠EAD=∠ADE,所以∠ADE=∠ECF,则AD=AC=5,AB=
,在Rt△OAB中利用勾股定理计算出OB=
,则OE=
OB=
,易得Rt△OEF∽Rt△OAB,利用相似比可计算出OF=
,于是得到F点坐标为(
,0).
②作BP⊥OA于P,根据圆周角定理得∠OBA=90°,根据含30度的直角三角形三边的关系得到BP=
| 5 |
| 2 |
(2)连结OD,由AB=BD,AB⊥OB,根据等腰三角形的判定方法得到△ODA为等腰三角形,则CB=
| 1 |
| 2 |
①当Rt△ECF∽Rt△AOB时有∠AOB=∠ECF,则EO=EC,所以OF=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 6 |
| 35 |
| 6 |
| 35 |
| 6 |
②当Rt△ECF∽Rt△AEB,连结BF,由∠EFA=∠EBA=90°得到点E、F、A、B共圆,根据圆周角定理得∠AEB=∠AFB,而∠AFB=∠ECF,所以CE∥BF,则OC:OF=OE:OB=2:3,可计算出OF=
| 15 |
| 2 |
| 15 |
| 2 |
| 5 |
| 2 |
5
| ||
| 2 |
| 2 |
| 3 |
5
| ||
| 3 |
| 25 |
| 4 |
| 25 |
| 4 |
解答: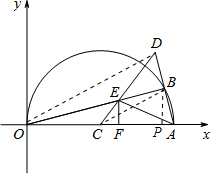 解:(1)如图,连接BC,
解:(1)如图,连接BC,
∵点A(10,0),
∴OC=AC=5,
∴∠ACB=2∠AOB=30°,
①弧AB的长为:
=
π;
②作BP⊥OA于P,如图,
∵OA是半圆C的直径,
∴∠OBA=90°,
∵∠ACB=30°,CB=5,
∴BP=
BC=
,
∴S△OAB=
×
×10=
;
(2)连结OD,
∵AB=BD,AB⊥OB,
∴△ODA为等腰三角形,
∴OD=OA=10,
∴CB=
OD,CB∥OD,
∴△BCE∽△ODE,
∴BE:OE=CE:DE=BC:OD=1:2,
①当Rt△ECF∽Rt△AOB,如图,
∴∠AOB=∠ECF,
∴EO=EC,
而EF⊥OC,
∴OF=
OC=
,
∴F点坐标为(
,0);
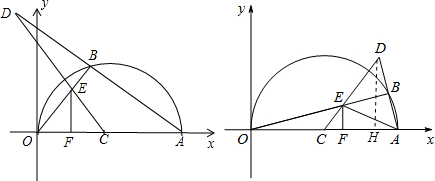 当Rt△ECF∽Rt△OAB,作DH⊥OA,如图,
当Rt△ECF∽Rt△OAB,作DH⊥OA,如图,
∴∠BAO=∠FCE,
∴DC=DA,
∴CH=AH=
CA=
,
∵EF∥DH,CE:DE=1:2,
∴CF:CH=CE:CD=1:3,
∴CF=
CH=
,
∴OF=OC+CF=
,
∴F点坐标为(
,0);
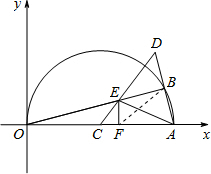 ②当Rt△ECF∽Rt△AEB,连结BF,如图,
②当Rt△ECF∽Rt△AEB,连结BF,如图,
∴∠ECF=∠AEB,
∵∠EFA=∠EBA=90°,
∴点E、F、A、B共圆,
∴∠AEB=∠AFB,
∴∠AFB=∠ECF,
∴CE∥BF,
∴OC:OF=OE:OB=2:3,
∴OF=
OC=
,
∴F点坐标为(
,0);
当Rt△ECF∽Rt△EAB,
∴∠ECF=∠EAB,
∵∠EBA=90°,AB=DB,
∴△EAD为等腰三角形,
∴∠EAD=∠ADE,
∴∠ADE=∠ECF,
∴AD=AC=5,
∴AB=
,
在Rt△OAB中,OB=
=
,
∴OE=
OB=
,
∵Rt△OEF∽Rt△OAB,
∴OF:OB=OE:OA,
∴OF=
=
,
∴F点坐标为(
,0).
 解:(1)如图,连接BC,
解:(1)如图,连接BC,∵点A(10,0),
∴OC=AC=5,
∴∠ACB=2∠AOB=30°,
①弧AB的长为:
| 30π×5 |
| 180 |
| 5 |
| 6 |
②作BP⊥OA于P,如图,
∵OA是半圆C的直径,
∴∠OBA=90°,
∵∠ACB=30°,CB=5,
∴BP=
| 1 |
| 2 |
| 5 |
| 2 |
∴S△OAB=
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 2 |
(2)连结OD,
∵AB=BD,AB⊥OB,
∴△ODA为等腰三角形,
∴OD=OA=10,
∴CB=
| 1 |
| 2 |
∴△BCE∽△ODE,
∴BE:OE=CE:DE=BC:OD=1:2,
①当Rt△ECF∽Rt△AOB,如图,
∴∠AOB=∠ECF,
∴EO=EC,
而EF⊥OC,
∴OF=
| 1 |
| 2 |
| 5 |
| 2 |
∴F点坐标为(
| 5 |
| 2 |
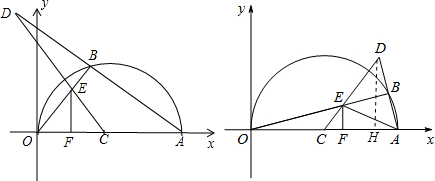 当Rt△ECF∽Rt△OAB,作DH⊥OA,如图,
当Rt△ECF∽Rt△OAB,作DH⊥OA,如图,∴∠BAO=∠FCE,
∴DC=DA,
∴CH=AH=
| 1 |
| 2 |
| 5 |
| 2 |
∵EF∥DH,CE:DE=1:2,
∴CF:CH=CE:CD=1:3,
∴CF=
| 1 |
| 3 |
| 5 |
| 6 |
∴OF=OC+CF=
| 35 |
| 6 |
∴F点坐标为(
| 35 |
| 6 |
 ②当Rt△ECF∽Rt△AEB,连结BF,如图,
②当Rt△ECF∽Rt△AEB,连结BF,如图,∴∠ECF=∠AEB,
∵∠EFA=∠EBA=90°,
∴点E、F、A、B共圆,
∴∠AEB=∠AFB,
∴∠AFB=∠ECF,
∴CE∥BF,
∴OC:OF=OE:OB=2:3,
∴OF=
| 3 |
| 2 |
| 15 |
| 2 |
∴F点坐标为(
| 15 |
| 2 |
当Rt△ECF∽Rt△EAB,
∴∠ECF=∠EAB,
∵∠EBA=90°,AB=DB,
∴△EAD为等腰三角形,
∴∠EAD=∠ADE,
∴∠ADE=∠ECF,
∴AD=AC=5,
∴AB=
| 5 |
| 2 |
在Rt△OAB中,OB=
| OA2-AB2 |
5
| ||
| 2 |
∴OE=
| 2 |
| 3 |
5
| ||
| 3 |
∵Rt△OEF∽Rt△OAB,
∴OF:OB=OE:OA,
∴OF=
| ||||||||
| 10 |
| 25 |
| 4 |
∴F点坐标为(
| 25 |
| 4 |
点评:本题考查了圆的综合题:熟练掌握圆周角定理和等腰三角形的判定与性质,并且会运用勾股定理和相似比进行几何计算;同时掌握分类讨论思想的运用.

练习册系列答案
相关题目
 (2012•衢州二模)如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米,两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D.
(2012•衢州二模)如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米,两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D. 、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题:
、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题: (2012•衢州二模)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=
(2012•衢州二模)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=