题目内容
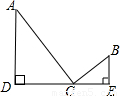
 将两个直角三角形纸片按如图所示的方法摆放(D、C、E在一条直线上),若AD·BE=DC·CE,求证:AC⊥CB.
将两个直角三角形纸片按如图所示的方法摆放(D、C、E在一条直线上),若AD·BE=DC·CE,求证:AC⊥CB.
证明:∵AD•BE=DC•CE,
∴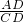 =
= ,
,
又∠ADC=∠BEC=90°,
∴△ADC∽△CEB,
∴∠A=∠BCE,
又∠A+∠ACD=90°,
∴∠BCE+∠ACD=90°,
∴∠ACB=90°,
即AC⊥CB.
分析:首先利用比例的性质得出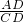 =
= ,进而得出△ADC∽△CEB,再利用相似三角形的性质得出∠ACB=90°即可得出答案.
,进而得出△ADC∽△CEB,再利用相似三角形的性质得出∠ACB=90°即可得出答案.
点评:此题主要考查了相似三角形的判定与性质,根据已知得出△ADC∽△CEB是解题关键.
∴
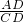 =
= ,
,又∠ADC=∠BEC=90°,
∴△ADC∽△CEB,
∴∠A=∠BCE,
又∠A+∠ACD=90°,
∴∠BCE+∠ACD=90°,
∴∠ACB=90°,
即AC⊥CB.
分析:首先利用比例的性质得出
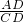 =
= ,进而得出△ADC∽△CEB,再利用相似三角形的性质得出∠ACB=90°即可得出答案.
,进而得出△ADC∽△CEB,再利用相似三角形的性质得出∠ACB=90°即可得出答案.点评:此题主要考查了相似三角形的判定与性质,根据已知得出△ADC∽△CEB是解题关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目

 24、如图,有一腰长为5,底边长为4的等腰三角形纸片,现沿着等腰三角形底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中,是四边形的共有( )
24、如图,有一腰长为5,底边长为4的等腰三角形纸片,现沿着等腰三角形底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中,是四边形的共有( ) 将两个直角三角形纸片按如图所示的方法摆放(D、C、E在一条直线上),若AD•BE=DC•CE,求证:AC⊥CB.
将两个直角三角形纸片按如图所示的方法摆放(D、C、E在一条直线上),若AD•BE=DC•CE,求证:AC⊥CB.