题目内容
不能判定△ABC与△DEF相似的题设是
- A.∠A=∠D,∠B=∠F
- B.
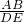 =
= ,∠B=∠D
,∠B=∠D - C.
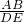 =
= =
=
- D.
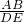 =
= ,∠B=∠D
,∠B=∠D
D
分析:相似的判定有三种方法:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
解答:A、∠A=∠D,∠B=∠F,可以判定△ABC与△DEF相似;
B、利用两边及其夹角的方法可判定△ABC与△DEF相似;
C、利用三边法可以判定△ABC与△DEF相似;
D、不能判定相似,因为∠B、∠D不是这两组边对应的夹角;
故选D.
点评:本题考查了相似三角形的判定,掌握相似三角形判定的三种方法是解答本题的关键.
分析:相似的判定有三种方法:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
解答:A、∠A=∠D,∠B=∠F,可以判定△ABC与△DEF相似;
B、利用两边及其夹角的方法可判定△ABC与△DEF相似;
C、利用三边法可以判定△ABC与△DEF相似;
D、不能判定相似,因为∠B、∠D不是这两组边对应的夹角;
故选D.
点评:本题考查了相似三角形的判定,掌握相似三角形判定的三种方法是解答本题的关键.

练习册系列答案
相关题目
下列条件,不能判定△ABC与△DEF相似的是( )
| A、∠C=∠F=90°,∠A=55°,∠D=35° | ||||
| B、∠C=∠F=90°,AB=10,BC=6,DE=15,EF=9 | ||||
C、∠C=∠F=90°,
| ||||
D、∠B=∠E=90°,
|
 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )A、
| ||||
| B、∠B=∠ADE | ||||
C、
| ||||
| D、∠C=∠AED |
下列各组条件中,不能判定△ABC与△A′B′C′相似的是( )
| A、AB=4cm,BC=8cm,AC=7cm,A'B'=2cm,B'C'=4cm,A'C'=3.5cm | B、∠A=42°,∠B=118°,∠A'=118°,∠B'=20° | C、AB=4cm,AC=3.2cm,∠B=50°,A'B'=2cm,A'C'=1.6cm,∠B'=50° | D、AB=8,AC=4,∠A=105°,A'C'=16,B'C'=8,∠C'=105° |
如图,由下列条件不能判定△ABC与△ADE相似的是( )
A. | B.∠B=∠ADE | C. | D.∠C=∠AED |