Question

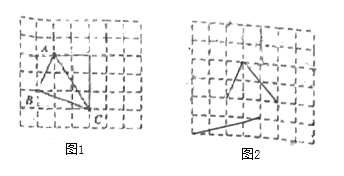
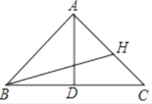
【题目】如图，在△ABC中，AB＝10，BC＝12，BC边上的中线AD＝8．

（1）证明：△ABC为等腰三角形；

（2）点H在线段AC上，试求AH＋BH＋CH的最小值．

Answer 1

【答案】(1)证明见解析；(2)19.6

【解析】

(1)由三角形的中线定义可知BD=DC=6，然后根据勾股定理的逆定理可证明△ABD为直角三角形，故AD⊥BC，则AD为BC的垂直平分线，依据线段垂直平分线的性质可知AB=AC;

(2)由题意可得到CH+AC=AC=10，故当BH最小时，AH+BH+CH有最小值，依据垂线段的性质可知当BH⊥AC时，BH有最小值，在△ABC中，依据面积法可求得BH的最小值．

(1)证明：∵AD是BC边上的中线，

∴BD=DC=6，

∵AB=10，BD=6，AD=8，

∴BD2+AD2=62+82=102，

∴△ABD是直角三角形，

∴AD⊥BC，

∵AD⊥BC，BD=DC，

∴AB=AC，

∴△ABC是等腰三角形．

(2)解：∵AH+BH+CH=BH+AC=BH+10，

∴当BH最小时，AH+BH+HC有最小值，

由垂线段的性质可知：当BH⊥AC时，BH有最小值，

∴，

∴，

∴BH=9.6，

∴AH+BH+HC的最小值为：10+9.6=19.6．