题目内容
已知一直角三角形的木板,三边的平方和为800cm2,则斜边长为 .
考点:勾股定理
专题:
分析:设出直角三角形的两直角边分别为a,b,斜边为c,利用勾股定理列出关系式,再由三边的平方和为1800,列出关系式,联立两关系式,即可求出斜边的长.
解答:解:设直角三角形的两直角边分别为acm,bcm,斜边为ccm,
根据勾股定理得:a2+b2=c2,
∵a2+b2+c2=800,
∴2c2=800,即c2=400,则c=20cm.
故答案为:20cm.
根据勾股定理得:a2+b2=c2,
∵a2+b2+c2=800,
∴2c2=800,即c2=400,则c=20cm.
故答案为:20cm.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
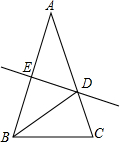 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )| A、①②③ | B、①②④ |
| C、②③④ | D、①③④ |
如果|a+2|+(b-1)2=0,那么(a+b)2014的值是( )
| A、-2014 | B、2014 |
| C、-1 | D、1 |
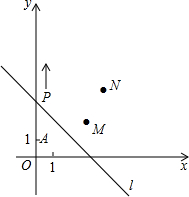 如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.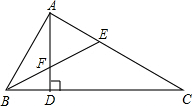 如图所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F,试判断△AEF的形状,并说明理由.
如图所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F,试判断△AEF的形状,并说明理由.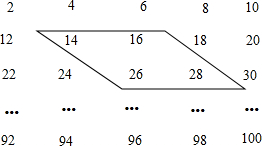 下列数阵是由50个偶数排成的.
下列数阵是由50个偶数排成的.