Question

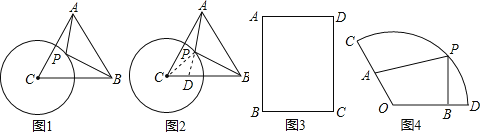
【题目】如图，等腰△ABC 纸板中， AB =AC=5 ， BC = 2 ，P为AB上一点，过P沿直线剪下一个与△ABC 相似的小三角形纸板，恰有 3 种不同的剪法，那么BP长可以为（ ）．

A.3.6B.2.6C.1.6D.0.6

Answer 1

【答案】D

【解析】

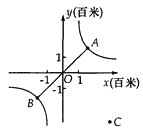
如图1中，过点P作PE∥BC交AC于E，PF∥AC交BC于F，则△APE∽△ABC，△BPF∽△BAC，得到两种方法．如图2中，作∠BP′G′=∠ACB时，△BP′G′∽△BCA，当C与G′重合时，则有BC2=BPBA，求出PB的值，即可判断满足条件的PB的值的范围．

如图1中，过点P作PE∥BC交AC于E，PF∥AC交BC于F，则△APE∽△ABC，△BPF∽△BAC，得到两种方法．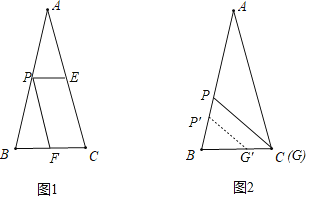

如图2中，作∠BP′G′=∠ACB时，△BP′G′∽△BCA，

当C与G′重合时，则有△BPC∽△BCA，

∴，

∴，

∵AB =AC=5 ， BC = 2 ，
∴，
∴，
∴当时，恰有3种不同的剪法，

∵0.6符合题意，
故选：D．