题目内容
 如图,圆外切等腰梯形ABCD的中位线EF=15cm,那么等腰梯形ABCD的周长等于
如图,圆外切等腰梯形ABCD的中位线EF=15cm,那么等腰梯形ABCD的周长等于
- A.15cm
- B.20cm
- C.30cm
- D.60cm
D
分析:首先根据梯形的中位线定理,求得梯形的两底和;再根据圆外切四边形的两组对边和相等,求得梯形的两腰和,从而求得梯形的周长.
解答:根据梯形的中位线等于两底和的一半,得梯形的两底和等于梯形的中位线的2倍,即30cm;
根据圆外切四边形的两组对边和相等,得梯形的两腰的和等于两底和,即30cm.
则梯形的周长等于30+30=60(cm).
故选D.
点评:此题综合运用了圆外切四边形的性质和梯形的中位线定理.
分析:首先根据梯形的中位线定理,求得梯形的两底和;再根据圆外切四边形的两组对边和相等,求得梯形的两腰和,从而求得梯形的周长.
解答:根据梯形的中位线等于两底和的一半,得梯形的两底和等于梯形的中位线的2倍,即30cm;
根据圆外切四边形的两组对边和相等,得梯形的两腰的和等于两底和,即30cm.
则梯形的周长等于30+30=60(cm).
故选D.
点评:此题综合运用了圆外切四边形的性质和梯形的中位线定理.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
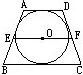
 19、如图,圆外切等腰梯形ABCD的中位线EF=15cm,那么等腰梯形ABCD的周长等于( )
19、如图,圆外切等腰梯形ABCD的中位线EF=15cm,那么等腰梯形ABCD的周长等于( )

