题目内容
16．设a、b是直角三角形的两条直角边，若该直角三角形的周长为6，斜边长为2.5，则ab的值是3．分析 根据勾股定理得出a2+b2的值，再利用完全平方公式求出ab的值．
解答 解：∵a、b是直角三角形的两条直角边，直角三角形的周长为6，斜边长为2.5，
∴a+b=3.5，a2+b2=2.52=6.25，
（a+b）2=12.25，
∴a2+b2+2ab=12.25，
∴2ab=6，
解得：ab=3．
故答案为：3．
点评 此题主要考查了勾股定理以及完全平方公式，正确应用完全平方公式是解题关键．
练习册系列答案
相关题目
7．
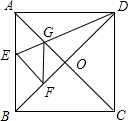如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，A恰好与BD上的点F重合，展开后，折痕DE分别交AB，AC于点E、G，连接GF，有下列结论：①∠AGD=112.5°；②AD=2AE；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG．其中正确结论的序号是（ ）
如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，A恰好与BD上的点F重合，展开后，折痕DE分别交AB，AC于点E、G，连接GF，有下列结论：①∠AGD=112.5°；②AD=2AE；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG．其中正确结论的序号是（ ）| A． | ①②③ | B． | ①③④ | C． | ①④⑤ | D． | ①②③④⑤ |
4．某工程甲单独做x天完成，乙单独做比甲慢3天完成，现由甲、乙合作5天后，余下的工程由甲单独做3天才能全部完成，则下列方程中符合题意的是（ ）
| A． | $\frac{8}{x}+\frac{5}{x-3}=1$ | B． | $（\frac{1}{x}+\frac{1}{x+3}）×5+\frac{3}{x}=1$ | C． | $\frac{3}{x-3}+5（\frac{1}{x-3}+\frac{1}{x}）=1$ | D． | $\frac{5}{x+（x+3）}+\frac{3}{x}=1$ |
1．某服装专卖店销售的甲品牌西服去年销售总额为50000元，今年每件西服售价比去年便宜400元，若售出的西服件数相同，则销售总额将比去年降低20%．
（1）求今年甲品牌西服的每件售价．
（2）若该服装店计划需要增进一批乙品牌西服，且甲、乙两种品牌西服共60件，而且乙品牌西服的进货件数不超过甲品牌件数的2倍，请设计出获利最多的进货方案．
附：今年乙品牌和甲品牌西服的进货和售价如表：
（1）求今年甲品牌西服的每件售价．
（2）若该服装店计划需要增进一批乙品牌西服，且甲、乙两种品牌西服共60件，而且乙品牌西服的进货件数不超过甲品牌件数的2倍，请设计出获利最多的进货方案．
附：今年乙品牌和甲品牌西服的进货和售价如表：
| 甲品牌 | 乙品牌 | |
| 进价（元/件） | 1100 | 1400 |
| 售价（元/件） | - | 2000 |
5．
如图，直线a∥b，∠1=120°，则∠2的度数是（ ）
如图，直线a∥b，∠1=120°，则∠2的度数是（ ）| A． | 120° | B． | 80° | C． | 60° | D． | 50° |
如图，直线CD上有一点O，过点O作OA⊥CD，OB平分∠AOD，则∠BOC的度数是135°．