Question

如图，抛物线y＝－x²＋bx＋c与x轴交于A、B两点，与y轴交于点C，点O为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF＝2，EF＝3．
(1)求抛物线所对应的函数解析式；(2)求△ABD的面积(3)将△AOC绕点C逆时针旋转90°，点A对应点为点G，问点G是否在该抛物线上？请说明理由．

Answer 1

（1）y=-x2+2x+3  (2) S_△ABD=8  (3)点G不在图像上。

解析试题分析：解：(1)∵四边形OCEF为矩形，OF＝2，EF＝3，
∴点C的坐标为(0，3)，点E的坐标为(2，3)．
把x＝0，y＝3；x＝2，y＝3分别代入y＝－x²＋bx＋c中，
得，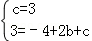
解得，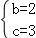
∴抛物线所对应的函数解析式为y＝－x²＋2x＋3；
(2)∵y＝－x²＋2x＋3＝－(x－1)²＋4，
∴抛物线的顶点坐标为D(1，4)，
∴△ABD中AB边的高为4，
令y＝0，得－x²＋2x＋3＝0，
解得x₁＝－1，x₂＝3，
所以AB＝3－(－1)＝4，
∴△ABD的面积＝×4×4＝8；
(3)△AOC绕点C逆时针旋转90°，CO落在CE所在的直线上，由(2)可知OA＝1，
∴点A对应点G的坐标为(3，2)，
当x＝3时，y＝－32＋2×3＋3＝0≠2，所以点G不在该抛物线上．
考点：二次函数的图像及性质，三角形面积公式，矩形的性质。
点评：熟知上述知识点，结合已知求得，题有三问较多，1,2问较为简单，3问需要验证，得到的结论与题目不符合，所以，可求之，本题有一定的难度，偏难，但难度不是很大，属于中档题。