Question

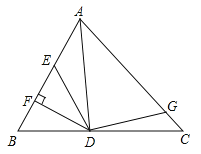
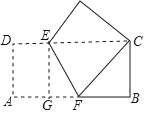
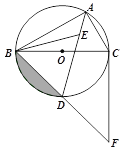
【题目】如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H，给出下列结论：①△DFP～△BPH；②；③PD2=PHCD；④，其中正确的是______（写出所有正确结论的序号）．

Answer 1

【答案】①②③

【解析】

依据∠FDP=∠PBD，∠DFP=∠BPC=60°，即可得到△DFP∽△BPH；依据△DFP∽△BPH，可得，再根据BP=CP=CD，即可得到；判定△DPH∽△CPD，可得，即PD2=PHCP，再根据CP=CD，即可得出PD2=PHCD；根据三角形面积计算公式，结合图形得到△BPD的面积=△BCP的面积+△CDP面积﹣△BCD的面积，即可得出．

∵PC=CD，∠PCD=30°，

∴∠PDC=75°，

∴∠FDP=15°，

∵∠DBA=45°，

∴∠PBD=15°，

∴∠FDP=∠PBD，

∵∠DFP=∠BPC=60°，

∴△DFP∽△BPH，故①正确；

∵∠DCF=90°﹣60°=30°，

∴tan∠DCF=，

∵△DFP∽△BPH，

∴，

∵BP=CP=CD，

∴，故②正确；

∵PC=DC，∠DCP=30°，

∴∠CDP=75°，

又∵∠DHP=∠DCH+∠CDH=75°，

∴∠DHP=∠CDP，而∠DPH=∠CPD，

∴△DPH∽△CPD，

∴，即PD2=PHCP，

又∵CP=CD，

∴PD2=PHCD，故③正确；

如图，过P作PM⊥CD，PN⊥BC，

设正方形ABCD的边长是4，△BPC为正三角形，则正方形ABCD的面积为16，

∴∠PBC=∠PCB=60°，PB=PC=BC=CD=4，

∴∠PCD=30°

∴PN=PBsin60°=4×=2，PM=PCsin30°=2，

∵S△BPD=S四边形PBCD﹣S△BCD=S△PBC+S△PDC﹣S△BCD

=×4×2+×2×4﹣×4×4

=4+4﹣8

=4﹣4，

∴，故④错，

故答案为：①②③．