题目内容
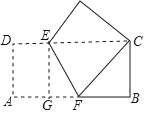
【题目】如图，把长方形纸片ABCD折叠，使顶点A与顶点C重合在一起，EF为折痕．若AB=9，BC=3，试求以折痕EF为边长的正方形面积（ ）
A. 11 B. 10 C. 9 D. 16
【答案】B
【解析】
根据矩形和折叠性质可得△EHC≌△FBC，从而可得BF=HE=DE，设BF=EH=DE=x，则AF=CF=9﹣x，在Rt△BCF中，由BF2+BC2=CF2可得BF=DE=AG=4，据此得出GF=1，由EF2=EG2+GF2可得答案．
如图，∵四边形ABCD是矩形，
∴AD=BC，∠D=∠B=90°，
根据折叠的性质，有HC=AD，∠H=∠D，HE=DE，
∴HC=BC，∠H=∠B，
又∠HCE+∠ECF=90°，∠BCF+∠ECF=90°，
∴∠HCE=∠BCF，
在△EHC和△FBC中，
∵
，
∴△EHC≌△FBC，
∴BF=HE，
∴BF=HE=DE，
设BF=EH=DE=x，
则AF=CF=9﹣x，
在Rt△BCF中，由BF2+BC2=CF2可得x2+32=（9﹣x）2，
解得：x=4，即DE=EH=BF=4，
则AG=DE=EH=BF=4，
∴GF=AB﹣AG﹣BF=9﹣4﹣4=1，
∴EF2=EG2+GF2=32+12=10，
故选B．
练习册系列答案
名校课堂系列答案
相关题目
