题目内容
1.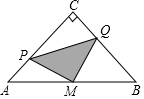 如图,在△ABC中,∠C=90°,AC=BC=4cm,M是AB的中点,点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,到点C、B时停止运动,设运动时间为t(s),△PMQ的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
如图,在△ABC中,∠C=90°,AC=BC=4cm,M是AB的中点,点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,到点C、B时停止运动,设运动时间为t(s),△PMQ的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )| A. | 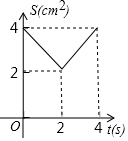 | B. | 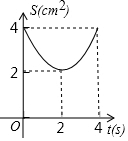 | C. | 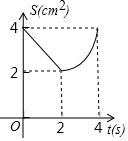 | D. | 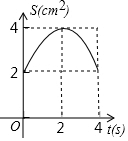 |
分析 由SAS证明△AMP≌△CMQ,得出△AMP的面积=△CMQ的面积,四边形CPMQ的面积=△ACM的面积=$\frac{1}{2}$△ABC的面积=4,求出△PMQ的面积=四边形CPMQ的面积-△PCQ的面积=$\frac{1}{2}$(t-2)2+2;由二次函数的图象即可得出答案.
解答 解:连接CM,如图所示:
根据题意得:AP=CQ=t,则PC=4-t,
∵∠C=90°,AC=BC=4cm,M是AB的中点,
∴∠A=∠B=∠MCQ=45°,CM=$\frac{1}{2}$AB=AM=BM,
在△AMP和△CMQ中,$\left\{\begin{array}{l}{AP=CQ}&{\;}\\{∠A=∠MCQ}&{\;}\\{AM=CM}&{\;}\end{array}\right.$,
∴△AMP≌△CMQ(SAS),
∴△AMP的面积=△CMQ的面积,
∴四边形CPMQ的面积=△ACM的面积=$\frac{1}{2}$△ABC的面积=$\frac{1}{2}$×$\frac{1}{2}$×4×4=4,
∴△PMQ的面积S=四边形CPMQ的面积-△PCQ的面积=4-$\frac{1}{2}$t×(4-t)=$\frac{1}{2}$t2-2t+4=$\frac{1}{2}$(t-2)2+2;
由二次函数的图象得:选项B正确;
故选:B.
点评 此题主要考查了动点问题的函数图象、等腰直角三角形的性质、全等三角形的判定与性质以及三角形面积的计算;熟练掌握等腰直角三角形的性质,证明三角形全等和求出S与t的函数关系式是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.将2.05×10-3用小数表示为( )
| A. | 0.000205 | B. | 0.00205 | C. | 0.0205 | D. | -0.00205 |
12. 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )| A. | $\frac{AD}{AB}=\frac{AE}{AC}$ | B. | $\frac{DE}{FC}=\frac{AD}{BD}$ | C. | $\frac{AD}{BF}=\frac{AE}{FC}$ | D. | $\frac{BF}{BC}=\frac{AD}{AB}$ |
6. 如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
 如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
13.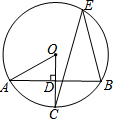 如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
 如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
10.面积为2的正方形的边长在( )
| A. | 1.5和2之间 | B. | 1和1.5之间 | C. | 0.5和1之间 | D. | 0和0.5之间 |
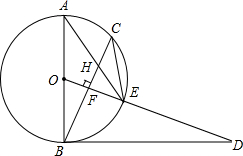 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.