��Ŀ����
��֪������������������y=| k |
| x |
| 1 |
| 4 |
��1��������������ͼ�����㣨2��2����
�����������ı���ʽ��
��֤��������������ͼ�����κ���ͼ��Ķ��㣮
��2���������y=
| 1 |
| 4 |
| 1 |
| 4 |
��������1���ٰ�x=2��y=2�ֱ�������������ı���ʽ���������k��a��ֵ�����ɵõ��������ı���ʽ������������κ���ͼ��Ķ������꣬�Ѷ���������뷴���������Ľ���ʽ���������Ƿ���ȼ��ɣ�
��2�������ڷ���������a��ֵ���������ȸ��ݸ����б�ʽ���a�ķ�Χ���跽��
x2+x+a=0�������ֱ�Ϊx1��x2�����ݸ���ϵ����ϵ�У�x1+x2=-4��x1•x2=4a�����
+
��ֵ�������a=1���������a��ȡֵ��Χa��1�����������жϴ𰸣�
��2�������ڷ���������a��ֵ���������ȸ��ݸ����б�ʽ���a�ķ�Χ���跽��
| 1 |
| 4 |
| 1 |
| x1 |
| 1 |
| x2 |
�����1���ٽ⣺�������⣬��x=2��y=2�ֱ�������������ı���ʽ��
��2=
��k=4��
���Է���������Ϊy=
��
��2=1+2+a��a=-1��
���Զ��κ���Ϊy=
x2+x-1��
���������ı���ʽ�ֱ���y=
��y=
x2+x-1��
��֤������y=
x2+x-1=
(x+2)2-2֪��
���κ���ͼ��Ķ�������Ϊ��-2��-2����
�ֵ�x=-2ʱ��y=
=-2��
���Է�����������ͼ�����κ���ͼ��Ķ��㣮
��2���⣺�����ڷ���������a��ֵ��
���ɣ��������⣬�ɡ�=1-4��
a��0��a��1��
��a��ȡֵ��Χ��a��1��
�跽��
x2+x+a=0�������ֱ�Ϊx1��x2��
�ɸ���ϵ����ϵ�У�
x1+x2=-4��x1•x2=4a��
��
+
=
=
=-
��
��-
=-1��
��a=1����a��1������
����ڷ���������a��ֵ��
�𣺲�����
��2=
| k |
| 2 |
���Է���������Ϊy=
| 4 |
| x |
��2=1+2+a��a=-1��
���Զ��κ���Ϊy=
| 1 |
| 4 |
���������ı���ʽ�ֱ���y=
| 4 |
| x |
| 1 |
| 4 |
��֤������y=
| 1 |
| 4 |
| 1 |
| 4 |
���κ���ͼ��Ķ�������Ϊ��-2��-2����
�ֵ�x=-2ʱ��y=
| 4 |
| -2 |
���Է�����������ͼ�����κ���ͼ��Ķ��㣮
��2���⣺�����ڷ���������a��ֵ��
���ɣ��������⣬�ɡ�=1-4��
| 1 |
| 4 |
��a��ȡֵ��Χ��a��1��
�跽��
| 1 |
| 4 |
�ɸ���ϵ����ϵ�У�
x1+x2=-4��x1•x2=4a��
��
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| -4 |
| 4a |
| 1 |
| a |
��-
| 1 |
| a |
��a=1����a��1������
����ڷ���������a��ֵ��
�𣺲�����
������������Ҫ����Զ��κ��������ʣ���һԪһ�η��̣������б�ʽ������ϵ���Ĺ�ϵ���ô���ϵ�����������������κ����Ľ���ʽ��֪ʶ�����������գ����ۺ�������Щ���ʽ��м����ǽ����Ĺؼ������ͽϺã��ۺ���ǿ��

��ϰ��ϵ�д�
 ��������ϵ�д�
��������ϵ�д�
�����Ŀ
 ��2013•��ɽ����֪����������y=ax�뷴��������
��2013•��ɽ����֪����������y=ax�뷴�������� ��֪����������y=ax�뷴��������
��֪����������y=ax�뷴��������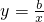 ��ͼ����һ��������A��1��2����
��ͼ����һ��������A��1��2����
 ��֪����������y=ax�뷴��������
��֪����������y=ax�뷴�������� ��ͼ����һ��������A��1��2����
��ͼ����һ��������A��1��2���� ��ͼ����һ��������A��1��2����
��ͼ����һ��������A��1��2����