Question

【题目】如果一个三角形的两条边的和是第三边的两倍，则称这个三角形是“优三角形”，这两条边的比称为“优比”（若这两边不等，则优比为较大边与较小边的比），记为.

（1）命题：“等边三角形为优三角形，其优比为1”，是真命题还是假命题？

（2）已知为优三角形，，，，

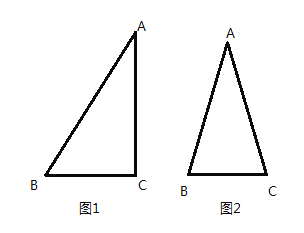
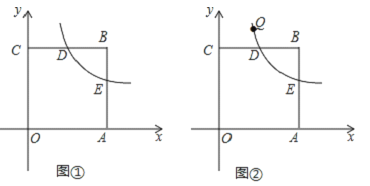
①如图1，若，，，求的值.

②如图2，若，求优比的取值范围.

（3）已知是优三角形，且，，求的面积.

Answer 1

【答案】（1）该命题是真命题，理由见解析；（2）①a的值为；②k的取值范围为；（3）的面积为或．

【解析】

（1）根据等边三角形的性质、优三角形和优比的定义即可判断；

（2）①先利用勾股定理求出c的值，再根据优三角形的定义列出的等式，然后求解即可；

②类似①分三种情况分析，再根据三角形的三边关系定理得出每种情况下之间的关系，然后根据优比的定义求解即可；

（3）如图（见解析），设，先利用直角三角形的性质、勾股定理求出AC、AB的长及面积的表达式，再类似（2），根据优三角形的定义分三种情况分别列出等式，然后解出x的值，即可得出的面积．

（1）该命题是真命题，理由如下：

设等边三角形的三边边长为a

则其中两条边的和为2a，恰好是第三边a的2倍，满足优三角形的定义，即等边三角形为优三角形

又因该两条边相等，则这两条边的比为1，即其优比为1

故该命题是真命题；

（2）①

根据优三角形的定义，分以下三种情况：

当时，，整理得，此方程没有实数根

当时，，解得

当时，，解得，不符题意，舍去

综上，a的值为；

②由题意得：均为正数

根据优三角形的定义，分以下三种情况：（）

当时，则

由三角形的三边关系定理得

则，解得，即

故此时k的取值范围为

当时，则

由三角形的三边关系定理得

则，解得，即

故此时k的取值范围为

当时，则

由三角形的三边关系定理得

则，解得，即

故此时k的取值范围为

综上，k的取值范围为；

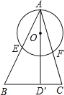
（3）如图，过点A作，则

设

是优三角形，分以下三种情况：

当时，即，解得

则

当时，即，解得

则

当时，即，整理得，此方程没有实数根

综上，的面积为或．