Question

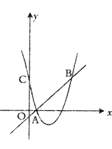
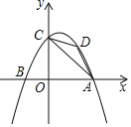
【题目】如图，二次函数y＝﹣x2+x+2交x轴于点A.B（A在B的右侧），与y轴交于点C，D为第一象限抛物线上的动点，则△ACD面积的最大值是_____

Answer 1

【答案】1

【解析】

先计算当x＝0时的函数值得到C（0，2），解方程﹣x2+x+2＝0得A（2，0），易得直线AC的解析式为y＝﹣x+2，作DE∥y轴交AC于E，如图，设D（t，﹣t2+t+2），则E（t，﹣t+2），利用三角形面积公式得到△ACD面积＝×2×DE＝﹣t2+2t，然后根据二次函数的性质解决问题．

当x＝0时，y＝﹣x2+x+2＝2，则C（0，2），

当y＝0时，﹣x2+x+2＝0，解得x1＝﹣1，x2＝2，则A（2，0），

易得直线AC的解析式为y＝﹣x+2，

作DE∥y轴交AC于E，如图，

设D（t，﹣t2+t+2），则E（t，﹣t+2），

∴DE＝﹣t2+t+2﹣（﹣t+2）＝﹣t2+2t，

∴△ACD面积＝×2×DE＝﹣t2+2t＝﹣（t﹣1）2+1，

当t＝1时，△ACD面积有最大值为1．

故答案为：1