题目内容
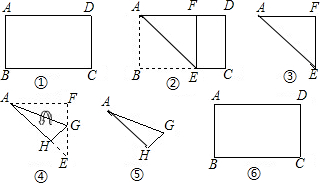
矩形纸片ABCD中，AD=10cm，AB=4cm，按如图方式折叠，使点B与点D重合，折痕为EF，则DE= cm．
【答案】分析：根据已知条件可以知道，DE=BE，若设DE=x，则DE=BE=x，AE=10-x，在Rt△ABE中可以利用勾股定理，列方程求出DE的长．
解答：解：设DE=x，则BE=DE=x，AE=10-x，
又∵在Rt△ABE中AB2+AE2=BE2，
即42+（10-x）2=x2，
解得x=
．
故答案为：
．
点评：在解决本题的过程中要注意折叠时出现的相等的线段，把求线段长的问题转化为解直角三角形的问题．
解答：解：设DE=x，则BE=DE=x，AE=10-x，
又∵在Rt△ABE中AB2+AE2=BE2，
即42+（10-x）2=x2，
解得x=
．故答案为：
．点评：在解决本题的过程中要注意折叠时出现的相等的线段，把求线段长的问题转化为解直角三角形的问题．
练习册系列答案
相关题目
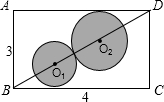如图，矩形纸片ABCD中，AB=3cm，BC=4cm，若要在该纸片中剪下两个外切的圆⊙O1和⊙O2，要求⊙O1和⊙O2的圆心均在对角线BD上，且⊙O1和⊙O2分别与BC、AD相切，则O1O2的长为（ ）
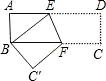如图，矩形纸片ABCD中，AD=9，AB=3，将其折叠，使点D与点B重合，折痕为EF，那么折痕EF的长为
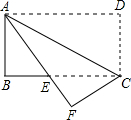如图，在矩形纸片ABCD中，将矩形纸片沿着对角线AC折叠，使点D落在点F处，设AF与BC相交于点E．
