题目内容
已知:在△ABC中,∠B=45°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.

(1)如图1,当点D在线段BC上时,CF是否满足条件“CF=BC﹣CD”,请给出证明过程。
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
(1)证明:①∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,
∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴BD⊥CF;
②由①△BAD≌△CAF可得BD=CF,
∵BD=BC-CD,
∴CF=BC-CD;
(2)CF=BC+CD;(3)①CF=CD-BC;②△AOC是等腰三角形.
【解析】
试题分析:(1)①根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,再根据正方形的性质可得AD=AF,∠DAF=90°,然后利用同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△BAD和△CAF全等,根据全等三角形对应角相等可得∠ACF=∠ABD,再求出∠ACF+∠ACB=90°,从而得证;②根据全等三角形对应边相等可得BD=CF,从而求出CF=BC-CD;
(2)与(1)同理可得BD=CF,然后结合图形可得CF=BC+CD;
(3)①与(1)同理可得BD=CF,然后结合图形可得CF=CD-BC;②根据等腰直角三角形的性质求出∠ABC=∠ACB=45°,再根据邻补角的定义求出∠ABD=135°,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△BAD和△CAF全等,根据全等三角形对应角相等可得∠ACF=∠ABD,再求出∠FCD=90°,然后根据直角三角形斜边上的中线等于斜边的一半求出OC= DF,再根据正方形的对角线相等求出OC=OA,从而得到△AOC是等腰三角形.
DF,再根据正方形的对角线相等求出OC=OA,从而得到△AOC是等腰三角形.
试题解析:(1)证明:①∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵ ∠BAC=∠BAD+∠DAC=90°,
∠BAC=∠BAD+∠DAC=90°,
∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF ,
,
在△BAD和△CAF中,
 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴BD⊥CF;
②由①△BAD≌△CAF可得BD=CF,
∵BD=BC-CD,
∴CF=BC-CD;
(2)与(1)同理可得BD=CF,
所以,CF=BC+CD;
(3)①与(1)同理可得,BD=CF,
所以,CF=CD-BC;
②∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
则∠ABD=180°-45°=135°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAF+∠CAF=90°,
∠DAF=∠BAD+∠BAF=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=180°-45°=135°,
∴∠FCD=∠ACF-∠ACB=90°,
则△FCD为直角三角形,
∵正方形ADEF中,O为DF中点,
∴OC= DF,
DF,
∵在正方形ADEF中,OA= AE,AE=DF,
AE,AE=DF,
∴OC=OA,
∴△AOC是等腰三角形.

下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 与方差s2:
与方差s2:
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 561 | 560 | 561 | 560 |
| 方差s2(cm2) | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心。重心有很多美妙的性质,如有关线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题。
请你利用重心的概念完成如下问题:
 |
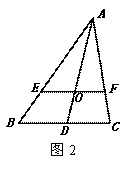
(1)如图1,△ABC的中线AD、CE的交点O为三角形的重心,利用三角形的中位线可以证明: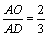 ,请你完成该证明;
,请你完成该证明;
(2)运用第(1)的结论解决以下问题:
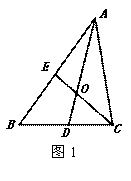
①小丽说:“过三角形的重心任画一条直线都能将三角形的面积平分”。小 明想了想说:“这个说法是错误的。”他过点O画出了BC的平行线,交AB、AC于点E、F,如图2,你能求出
明想了想说:“这个说法是错误的。”他过点O画出了BC的平行线,交AB、AC于点E、F,如图2,你能求出 的值吗?谁的说法正确?
的值吗?谁的说法正确?
②△ABC中,∠C=90°,AB=6cm,求△ABC的重心与外心的距离。
 ;
; 小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是 .
小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是 .
