Question

【题目】如图，在边长均为1的小正方形网格纸中，△OAB的顶点O，A，B均在格点上，且O是直角坐标系的原点，点A在轴上．

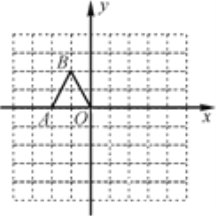
（1）以O为位似中心，将△OAB放大，使得放大后的△OA1B1与△OAB对应线段的比为2∶1，画出△OA1B1

(所画△OA1B1与△OAB在原点两侧)；

（2）直接写出点A1、B1的坐标______________________.

（3）直接写出____________.

Answer 1

【答案】（1）画图见解析；（2）；（3）

【解析】试题分析：

（1）如下图，延长AO至A1点，是OA1=2OA即可得到点A1，用同样的方法作出

点B1，再连接A1B1即可得到所求△OA1B1；

（2）根据所画图形写出点A1，B1的坐标即可；

（3）过点B1作B1D⊥x轴于点D，再由图形中所提供的数据信息即可写出tan∠OA1B1的值.

试题解析：

（1）所求△OA1B1如下图所示：

（2）如图，点A1的坐标为（4，0），点B1的坐标为（2，-4）；

（3）如图，过点B1作B1D⊥x轴于点D，则（2）可知，A1D=2，B1D=4，

∴tan∠OA1B1=.