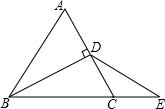
题目内容
 如图,BD=
如图,BD=| 1 | 2 |
分析:根据已知条件BD=
BC,可以得知点D是BC边上的中点,所以,BC边上的中线是AD;又由图中得知,△ABD、△ABC同高,根据三角形的面积公式求解即可.
| 1 |
| 2 |
解答:解:①∵BD=
BC,
∴BD=CD,
∴点D是边BC的中点,
∴BC边上的中线为AD;
②设△ABC的边BC上的高为h,则
S△ABC=
BC•h,
S△ABD=
BD•h,
又∵BD=
BC,
∴S△ABD=
S△ABC.
故答案为:AD,
S△ABC.
| 1 |
| 2 |
∴BD=CD,
∴点D是边BC的中点,
∴BC边上的中线为AD;
②设△ABC的边BC上的高为h,则
S△ABC=
| 1 |
| 2 |
S△ABD=
| 1 |
| 2 |
又∵BD=
| 1 |
| 2 |
∴S△ABD=
| 1 |
| 2 |
故答案为:AD,
| 1 |
| 2 |
点评:本题考查了三角形的面积,解得本题的关键是理解三角形中中线的定义,三角形的面积的求法.

练习册系列答案
相关题目
 如图,BD是等边△ABC边AC上的高,E是BC延长线上一点,且
如图,BD是等边△ABC边AC上的高,E是BC延长线上一点,且 如图,BD是等边△ABC的高,E是BC延长线上一点,且
如图,BD是等边△ABC的高,E是BC延长线上一点,且