题目内容
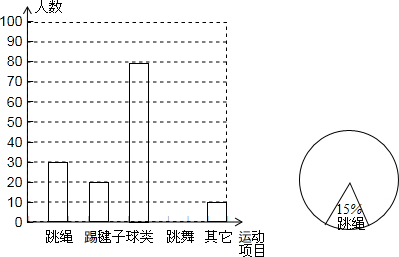
 如图,四边形ABCD内接于大圆O,且各边与小圆相切于点E,F,G,H.求证:四边形ABCD是正方形.
如图,四边形ABCD内接于大圆O,且各边与小圆相切于点E,F,G,H.求证:四边形ABCD是正方形.考点:正多边形和圆
专题:证明题
分析:连结OE、OF、OG、OH,利用切线的性质以及弦心距相等则弦相等可证明A、B、C、D是大圆O的四等分点,进而可证明四边形ABCD是正方形.
解答:证明:
连结OE、OF、OG、OH.
∵四边形ABCD与小圆分别切于点E、F、G、H,
∴OE=OF=OG=OH,OE⊥AB、OF⊥BC、OG⊥CD、OH⊥AD.
∴AB=BC=CD=DA.
∴A、B、C、D是大圆O的四等分点.
∴四边形ABCD是正方形.
连结OE、OF、OG、OH.
∵四边形ABCD与小圆分别切于点E、F、G、H,
∴OE=OF=OG=OH,OE⊥AB、OF⊥BC、OG⊥CD、OH⊥AD.
∴AB=BC=CD=DA.
∴A、B、C、D是大圆O的四等分点.
∴四边形ABCD是正方形.
点评:本题考查了正多边形与圆的关系,解题的关键是熟记把一个圆分成n(n是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
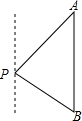 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )A、30
| ||
B、30
| ||
| C、60海里 | ||
D、30
|
下列说法中正确的是( )
| A、0没有倒数 |
| B、0没有相反数 |
| C、0没有绝对值 |
| D、平方为0的数不存在 |
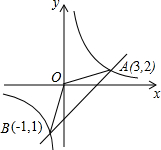 如图,反比例函数y=
如图,反比例函数y=