题目内容
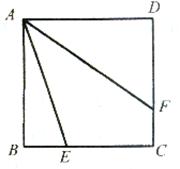 15、如图,已知下方形ABCD中,E为BC边上任意一点,AF平分∠DAE.求证:AE-BE=DF.
15、如图,已知下方形ABCD中,E为BC边上任意一点,AF平分∠DAE.求证:AE-BE=DF.分析:延长CB到G,使GB=DF,连接AG,易证△ADF≌△ABG,得到∠1=∠G,∠3=∠2=∠4,而∠1=∠4+∠5,则∠1=∠4+∠5=∠3+∠5=∠GAE,得到∠G=∠GAE,于是AE=GE=GB+BE=DF=BE,即可得到结论.
解答: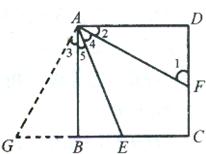 证明:延长CB到G,使GB=DF,连接AG(如图),
证明:延长CB到G,使GB=DF,连接AG(如图),
∵四边形ABCD为正方形,
∴AD=AB,
∴△ADF≌△ABG,
∴∠1=∠G,∠3=∠2=∠4,
又∵AB∥CD
∴∠1=∠4+∠5=∠3+∠5=∠GAE
∴∠G=∠GAE
∴AE=GE=GB+BE=DF+BE
所以AE-BE=DF.
 证明:延长CB到G,使GB=DF,连接AG(如图),
证明:延长CB到G,使GB=DF,连接AG(如图),∵四边形ABCD为正方形,
∴AD=AB,
∴△ADF≌△ABG,
∴∠1=∠G,∠3=∠2=∠4,
又∵AB∥CD
∴∠1=∠4+∠5=∠3+∠5=∠GAE
∴∠G=∠GAE
∴AE=GE=GB+BE=DF+BE
所以AE-BE=DF.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.同时考查了三角形全等的判定与性质.

练习册系列答案
相关题目
 1、如图,已知平行四边形ABCD,E是AB延长线上一点,连接DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,使△CDF≌△BEF,这个条件是
1、如图,已知平行四边形ABCD,E是AB延长线上一点,连接DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,使△CDF≌△BEF,这个条件是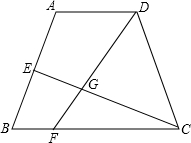 动点,线段CE与线段DF交于点G.
动点,线段CE与线段DF交于点G.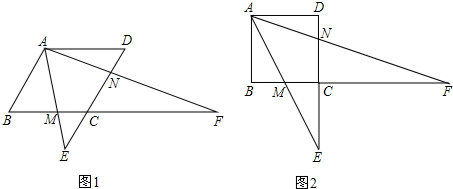
 (2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.
(2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.