题目内容
如图,已知等腰梯形ABCD中,AD∥BC,AD:BC=1:2,点E为边AB中点,点F是边BC上一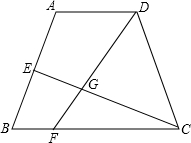 动点,线段CE与线段DF交于点G.
动点,线段CE与线段DF交于点G.(1)若
| BF |
| FC |
| 1 |
| 3 |
| DG |
| GF |
(2)连接AG,在(1)的条件下,写出线段AG和线段DC的位置关系和数量关系,并说明理由;
(3)连接AG,若AD=2,AB=3,且△ADG与△CDF相似,求BF的长.
分析:(1)延长CE和DA,相交于M,根据平行线分线段成比例进行计算可以求出
的值.(2)根据对应线段的比相等可以得到AG与DC的位置和数量关系.(3)根据两三角形相似,对应线段的比相等,求出线段BF的长.
| DG |
| GF |
解答:解:(1)∵BF:FC=1:3,∴设BF=k,
则FC=3k,BC=4k,∵AD:BC=1:2,∴AD=2k,
 如图:延长CE交DA的延长线于点M,
如图:延长CE交DA的延长线于点M,
∵AD∥BC,
∴
=
,且
=
∵点E为边AB中点,
∴AM=BC=4k,
∴DM=DA+AM=2k+4k=6k,
∴
=
=2.
(2)AG∥DC,且
=
.
证明:∵AD∥BC,
∴
=
=
,
∵
=
=
,
∴
=
,
∴AG∥DC.
∴
=
=
.
(3)∵ABCD是等腰梯形,AD=2,AD:BC=1:2,
∴BC=4,
∵AD∥BC,
∴∠ADG=∠DFC,
∵△ADG∽△CDF,
∴∠AGD=∠FDC或∠DAG=∠FDC.
情况1,当∠AGD=∠FDC时,有AG∥DC,延长CE交DA的延长线于点M,可得AM=4,
由
=
得
=
,
∴AG=2
∵△ADG与△CDF相似,且∠AGD=∠FDC,
∴
=
,即
=
,
∴CF=3
∴BF=1.
情况2,当∠DAG=∠FDC时,延长AG交BC于点T,可得△ABT∽△FCD,
则
=
,由AD∥BC得
=
=
,
设BF=x,可得FT=
,
∴
=
,
整理得:2x2-4x+11=0,
∵△=16-88<0,
∴无实数根;
∴BF=1.
则FC=3k,BC=4k,∵AD:BC=1:2,∴AD=2k,
 如图:延长CE交DA的延长线于点M,
如图:延长CE交DA的延长线于点M,∵AD∥BC,
∴
| AM |
| BC |
| AE |
| EB |
| DG |
| GF |
| DM |
| CF |
∵点E为边AB中点,
∴AM=BC=4k,
∴DM=DA+AM=2k+4k=6k,
∴
| DG |
| GF |
| 6 |
| 3 |
(2)AG∥DC,且
| AG |
| DC |
| 2 |
| 3 |
证明:∵AD∥BC,
∴
| MG |
| GC |
| DG |
| GF |
| 2 |
| 1 |
∵
| MA |
| AD |
| 4a |
| 2a |
| 2 |
| 1 |
∴
| MG |
| GC |
| MA |
| AD |
∴AG∥DC.
∴
| AG |
| DC |
| MA |
| MD |
| 2 |
| 3 |
(3)∵ABCD是等腰梯形,AD=2,AD:BC=1:2,
∴BC=4,
∵AD∥BC,
∴∠ADG=∠DFC,
∵△ADG∽△CDF,
∴∠AGD=∠FDC或∠DAG=∠FDC.
情况1,当∠AGD=∠FDC时,有AG∥DC,延长CE交DA的延长线于点M,可得AM=4,
由
| AG |
| DC |
| MA |
| MD |
| AG |
| 3 |
| 4 |
| 6 |
∴AG=2
∵△ADG与△CDF相似,且∠AGD=∠FDC,
∴
| AG |
| AD |
| DC |
| CF |
| 2 |
| 2 |
| 3 |
| CF |
∴CF=3
∴BF=1.
情况2,当∠DAG=∠FDC时,延长AG交BC于点T,可得△ABT∽△FCD,
则
| AB |
| BT |
| FC |
| CD |
| AD |
| FT |
| DG |
| GF |
| DM |
| CF |
设BF=x,可得FT=
| 4-x |
| 3 |
∴
| 3 | ||
x+
|
| 4-x |
| 3 |
整理得:2x2-4x+11=0,
∵△=16-88<0,
∴无实数根;
∴BF=1.
点评:本题考查的是相似三角形的判定与性质,(1)根据梯形的两底平行,延长CE和DA,运用平行线分线段成比例求出两线段的比.(2)根据对应线段的比相等,证明两线段互相平行.(3)根据两三角形相似,对应线段的比相等,求出线段BF的长.

练习册系列答案
相关题目
 ,
, 3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( )
3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( ) 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为
13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为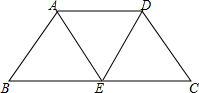 如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是
如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是