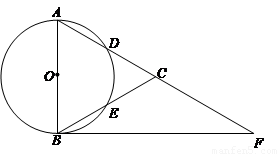题目内容
若a,b,c分别是三角形三边长,且满足
+
-
=
,则一定有( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a+b-c |
| A、a=b=c |
| B、a=b |
| C、a=c或b=c |
| D、a2+b2=c2 |
分析:本题先对
+
-
=
进行化简,然后再进行整理即可得出结果.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a+b-c |
解答:解:∵
+
-
=
,
∴bc(a+b-c)+ac(a+b-c)-ab(a+b-c)=abc,
即abc+b2c-bc2+a2c+abc-ac2-a2b-ab2+abc-abc=0,
合并得:b2c-bc2+a2c-ac2-a2b-ab2+2abc=0,
(a2b-a2c)+(-abc+ac2)+(ab2-abc)+(-b2c+bc2)=0,
a2(b-c)-ac(b-c)+ab(b-c)-bc(b-c)=0,
(a2-ac+ab-bc)(b-c)=0,
[a(a-c)+b(a-c)](b-c)=0,
∴(a+b)(a-c)(b-c)=0,
∴a=c或b=c,
故选C.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a+b-c |
∴bc(a+b-c)+ac(a+b-c)-ab(a+b-c)=abc,
即abc+b2c-bc2+a2c+abc-ac2-a2b-ab2+abc-abc=0,
合并得:b2c-bc2+a2c-ac2-a2b-ab2+2abc=0,
(a2b-a2c)+(-abc+ac2)+(ab2-abc)+(-b2c+bc2)=0,
a2(b-c)-ac(b-c)+ab(b-c)-bc(b-c)=0,
(a2-ac+ab-bc)(b-c)=0,
[a(a-c)+b(a-c)](b-c)=0,
∴(a+b)(a-c)(b-c)=0,
∴a=c或b=c,
故选C.
点评:本题主要考查了分式的混合运算,在解题时要注意知识的综合运用.

练习册系列答案
相关题目
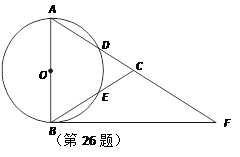
 (2013•龙岗区模拟)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(2013•龙岗区模拟)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. (2013•德州一模)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(2013•德州一模)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.