题目内容
已知: 中,
中, ,
, 中,
中, ,
, . 连接
. 连接 、
、 点
点 、、
、、 分别为
分别为 、
、 、
、 的中点.
的中点.
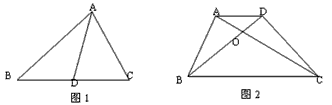
(1) 如图1,若 、
、 、
、 三点在同一直线上,且
三点在同一直线上,且 ,则
,则 的形状是__________,此时
的形状是__________,此时 ________;
________;
(2) 如图2,若 、
、 、
、 三点在同一直线上,且
三点在同一直线上,且 ,证明
,证明 ,并计算
,并计算 的值(用含
的值(用含 的式子表示);
的式子表示);
(3) 在图2中,固定 ,将
,将 绕点
绕点 旋转,直接写出
旋转,直接写出 的最大值.
的最大值.
(1)等边三角形,1
(2)
(3) 
解析试题分析:解:(1)等边三角形,1;(每空1分) ------------------------2分
(2)证明:连接 、
、 .
.
由题意,得 ,
, ,
, .
.
∵  、
、 、
、 三点在同一直线上,
三点在同一直线上,
∴  、
、 、
、 三点在同一直线上.
三点在同一直线上.
∴  .
.
∵  为
为 中点,
中点,
∴ 在Rt△ 中,
中, .
.
在Rt△ 中,
中, .
.
∴  .---------------------------3分
.---------------------------3分
∴  、
、 、
、 、
、 四点都在以
四点都在以 为圆心,
为圆心, 为半径的圆上.
为半径的圆上.
∴  .
.
又∵  ,
,
∴  .
.
∴  . ----------------------------------4分
. ----------------------------------4分
∴  .
.
由题意, ,又
,又 .
.
∴  .------------------------------------5分
.------------------------------------5分
∴  .
.
在Rt 中,
中, .
.
∵  ,
,
∴  .
.
∴  .------------------------------6分
.------------------------------6分
(3) .--------------------------------7分
.--------------------------------7分
考点:本题考查了和相似三角形的基本性质。
点评:这类问题很复杂,对于学有余力的学生来说可以深钻,解答这类试题的关键就在于巧妙地作出辅助线,辅助线找出来以后,试题便可迎刃而解。另外这类试题涉及的角度一般都是常见的特殊角,需要考生牢记,或者可以直接约分,所以一般不需在计算上出难题。

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

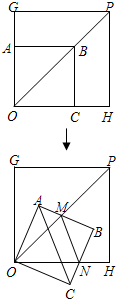 已知正方形AOCB和正方形GOHP的一个顶点O重合,边OA在OG上,边OC在OH上,正方形AOCB的边长为2.现将正方形AOCB绕O点顺时针旋转,当A点第一次落在OP直线上时停止旋转,旋转过程中,AB边交OP于点M,BC边交OH于点N.
已知正方形AOCB和正方形GOHP的一个顶点O重合,边OA在OG上,边OC在OH上,正方形AOCB的边长为2.现将正方形AOCB绕O点顺时针旋转,当A点第一次落在OP直线上时停止旋转,旋转过程中,AB边交OP于点M,BC边交OH于点N. 如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.
如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.