Question

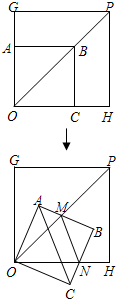已知正方形AOCB和正方形GOHP的一个顶点O重合，边OA在OG上，边OC在OH上，正方形AOCB的边长为2．现将正方形AOCB绕O点顺时针旋转，当A点第一次落在OP直线上时停止旋转，旋转过程中，AB边交OP于点M，BC边交OH于点N．
（1）求边OA在整个旋转过程中所扫过的面积；
（2）旋转过程中，当MN和AC平行时，求正方形AOCB旋转的度数；
（3）设△MBN的周长为k，在旋转正方形OABC的过程中，k值是否有变化？若无变化，请求出k的值；若变化，请说明理由．

Answer 1

分析：（1）根据正方形性质求出旋转的圆心角度和扇形的半径，根据扇形面积公式求出即可；
（2）求出BM=BN，推出AM=AN，证△OAM≌△OCN，推出∠AOM=∠CON，即可求出答案；
（3）根据全等三角形的性质求出AE=CN，求出NM=AM+CN，代入三角形的周长即可求出k=AB+BC=2+2=4．

解答：解：（1）∵四边形OGPH和四边形OACB是正方形，
∴∠GOP=∠POH=45°，OA=OC=2，
∴当A点第一次落在OP直线上，旋转的图形（扇形）的圆心角的度数是45°，半径是2，
∴边OA在整个旋转过程中所扫过的面积是

45•π•22

360

=

π

2

．

（2）解：∵MN∥AC，
∴∠BMN=∠BAC=45°，∠BNM=∠BCA=45°
∴∠BMN=∠BNM，
∴BM=BN，
由旋转可知：∠AOM=∠OCN，
又∵BA=BC，
∴AM=CN，
在△OAM和△OCN中

OA=OC ∠OAM=∠OCN AM=CN

∴△OAM≌△OCN（SAS），
∴∠AOM=∠CON，
∴∠AOM=

1

2

（90°-45°）=22.5°．

（3）k值无变化．   
延长BA交OG于E点，则∠AOE=45°-∠AOM=90°-45°-∠AOM=45°-∠AOM，
∴∠AOE=∠CON，
又∵OA=OC，∠OAE=∠CON，
在△OAE和△OCN中，

∠EAO=∠OCN OA=OC ∠EOA=∠CON

，
∴△OAE≌△OCN（ASA），
∴OE=ON，AE=CN，
在△OME和△OMN中，

OE=ON ∠EOM=∠NOM=45° OM=OM

，
∴△OME≌△OMN（SAS），
∴MN=ME=AM+AE，
∴MN=AM+CN，
∵△BMN的周长是k，
∴k=BM+BN+MN=BM+BN+AM+CN=AB+BC=2+2=4，
即k=4，
∴在旋转正方形OABC的过程中，k值无变化．

点评：本题考查了正方形性质，全等三角形的性质和判定，旋转的性质，扇形的面积的应用，主要考查学生综合运用性质进行推理和计算的能力．