题目内容
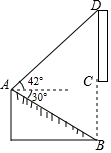
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,垂足为点
,垂足为点![]() .则以下结论:①
.则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,⑤
,⑤![]() ,其中正确的结论有( )
,其中正确的结论有( )
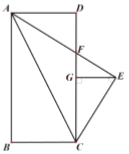
A.1个B.2个C.3个D.4个
【答案】D
【解析】
过点F作FH⊥AC,由角平分线的性质得到HF=DF,延长CE与AD的延长线交于点M,
又AF平分∠CAD,AF⊥CE,由“三线合一”逆定理,得到AC=AM,CE=EM.再设HF=DF=x,由等积法得到![]() ,从而求出关键的DF的值.利用勾股定理得到AC=AH=
,从而求出关键的DF的值.利用勾股定理得到AC=AH=![]() , 有DM=
, 有DM=![]() ,
,![]() ,所以CE=
,所以CE=![]() ,而后找到图中常见的相识三角形并利用其性质逐一推理计算判断即可.
,而后找到图中常见的相识三角形并利用其性质逐一推理计算判断即可.
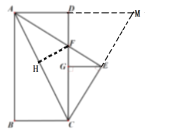
解:∵∠CEF=∠CEA=90°,∠CAE=∠EAD=∠FCE,
∴![]() ;
;
故① 对;
若![]() 成立,则易知∠BAC=∠EAC=∠FAD=30°,则在
成立,则易知∠BAC=∠EAC=∠FAD=30°,则在![]() 中BC=
中BC=![]() AB,而BC=2,AB=4,BC=
AB,而BC=2,AB=4,BC=![]() AB,故假设不成立. ②不对;
AB,故假设不成立. ②不对;
过点F作FH⊥AC,∵AF平分∠CAD,AD⊥DF,∴HF=DF=x,则CF=4-x,
又∵![]() ,
,
∵![]() ,
,
∴![]()
解得![]()
∴![]() ,
, ![]() ∴
∴![]() ,故④对;
,故④对;
又∵![]() ,
,
延长CE与AD的延长线交于点M,
∵AF平分∠CAD,AF⊥CE,
∴AC=AM=![]() ,CE=EM=
,CE=EM=![]() ,
,
∴DM=![]() ,又∵
,又∵![]()
∴![]()
∴![]() ,故③对;
,故③对;
∵∠CGE=∠ADF=90°,∠ECG=∠DAF,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴CG=DG=2,
又∵∠FEC=90°,GE⊥CF,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴ ![]() ,又∵CG=DG,
,又∵CG=DG,
∴![]() ∴⑤对;
∴⑤对;
综上有4个正确,
故选:D.

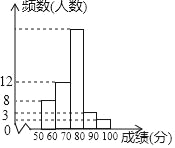
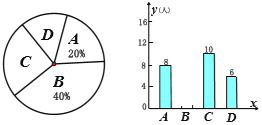
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.