题目内容
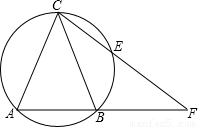
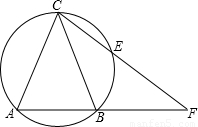
如图,以△ACF的边AC为弦的圆交AF、CF于点B、E,连接BC,且满足AC2=CE•CF.求证:△ABC为等腰三角形.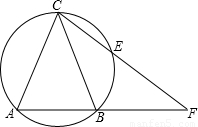
【答案】分析:连接AE,根据AC2=CE•CF及∠ACE=∠FCA,可求出△ACE∽△FCA,再根据相似三角形的对应角相等及圆周角定理可求出弧AC=弧BC,AC=BC即可解答.
解答: 证明:连接AE,
证明:连接AE,
∵AC2=CE•CF,
∴ ,
,
又∵∠ACE=∠FCA.
∴△ACE∽△FCA,
∴∠AEC=∠FAC.
∵弧AC=弧BC,
∴AC=BC,
∴△ABC为等腰三角形.
点评:此题涉及到圆周角定理及相似三角形判定与性质,解答此题的关键是连接AE,构造出相似三角形,再根据相似三角形的性质及圆周角定理即可解答.
解答:
 证明:连接AE,
证明:连接AE,∵AC2=CE•CF,
∴
 ,
,又∵∠ACE=∠FCA.
∴△ACE∽△FCA,
∴∠AEC=∠FAC.
∵弧AC=弧BC,
∴AC=BC,
∴△ABC为等腰三角形.
点评:此题涉及到圆周角定理及相似三角形判定与性质,解答此题的关键是连接AE,构造出相似三角形,再根据相似三角形的性质及圆周角定理即可解答.

练习册系列答案
相关题目
 如图,以△ACF的边AC为弦的圆交AF、CF于点B、E,连接BC,且满足AC2=CE•CF.求证:△ABC为等腰三角形.
如图,以△ACF的边AC为弦的圆交AF、CF于点B、E,连接BC,且满足AC2=CE•CF.求证:△ABC为等腰三角形.