题目内容
矩形ABCD的对角线相交于点O,DE∥AC,CE∥DB,CE、DE交于点E,请问:四边形DOCE是什么四边形?请说明理由.

考点:
菱形的判定;平行线的性质;矩形的性质.
专题:
探究型.
分析:
首先判断出DOCE是平行四边形,而ABCD是矩形,由OC、OD是矩形对角线的一半,知OC=OD,从而得出DOCE是菱形.
解答:
解:四边形DOCE是菱形.
理由:∵DE∥AC,CE∥DB,
∴四边形DOCE是平行四边形,
又∵四边形ABCD是矩形,
∴AC=BD,OC=OA=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴OC=OD,
∴四边形DOCE是菱形(一组邻边相等的平行四边形是菱形).
点评:
本题属于开放型试题,一般先从已知出发,推出一些中间结论,将它们结合起来,得出问题的结论.

练习册系列答案
相关题目

 如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为
如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为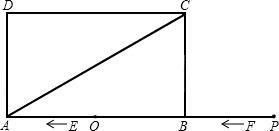 如图,矩形ABCD中,AB=6,BC=2
如图,矩形ABCD中,AB=6,BC=2 已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=5cm,则矩形对角线的长是
已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=5cm,则矩形对角线的长是