题目内容
如图所示,已知二次函数y=x2-4x+3的图象交x轴于A,B两点(点A在点B的左侧); 交y轴于点C。

(1)求直线BC的解析式;
(2)点D是在直线BC下方的抛物线上的一个动点,当△BCD的面积最大时,求D点坐标。
(1)y=-x+3;(2)( ,-
,- ).
).
【解析】
试题分析:(1)利用y=x2-4x+3的图象交x轴于A、B两点(点A在点B的左侧),抛物线y=x2-4x+3交y轴于点C,即可得出A,B,C点的坐标,将B,C点的坐标分别代入y=kx+b(k≠0),即可得出解析式;
(2)设过D点的直线与直线BC平行,且抛物线只有一个交点时,△BCD的面积最大.
试题解析:(1)设直线BC的解析式为:y=kx+b(k≠0).
令x2-4x+3=0,
解得:x1=1,x2=3,
则A(1,0),B(3,0),C(0,3),
将B(3,0),C(0,3),代入y=kx+b(k≠0),得
 ,
,
解得:k=-1,b=3,
BC所在直线为:y=-x+3;
(2)设过D点的直线与直线BC平行,且抛物线只有一个交点时,△BCD的面积最大.

∵直线BC为y=-x+3,∴设过D点的直线为y=-x+b,
∴ ,
,
∴x2-3x+3-b=0,
∴△=9-4(3-b)=0,
解得b= ,
,
∴ ,
,
解得,
 ,
,
则点D的坐标为:( ,-
,- ).
).
考点:1.抛物线与x轴的交点;2.待定系数法求一次函数解析式;3.二次函数图象上点的坐标特征.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 上,OC在
上,OC在 轴上,且
轴上,且 .
.
 的正方形ABCD的边CD在
的正方形ABCD的边CD在 轴上,A、B两点在抛物线上,请用含
轴上,A、B两点在抛物线上,请用含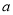 的代数式表示点B的坐标,并求出正方形边长
的代数式表示点B的坐标,并求出正方形边长 元,经过连续两次降价后售价为
元,经过连续两次降价后售价为 元,设平均每次降价的百分率为
元,设平均每次降价的百分率为 ,则满足
,则满足 的方程是( )
的方程是( ) B.
B.
 D.
D.


 C、∠AEC=2∠D D、∠B=∠C
C、∠AEC=2∠D D、∠B=∠C ),其中a=-2
),其中a=-2 xy+2)+4x²],其中x=-2,y=
xy+2)+4x²],其中x=-2,y=