题目内容
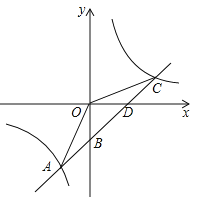
【题目】已知正比例函数y＝x的图象与反比例函数y＝
（k为常数，且k≠0）的图象有一个交点的纵坐标是2．
（Ⅰ）当x＝4时，求反比例函数y＝的值；
（Ⅱ）当﹣2＜x＜﹣1时，求反比例函数y＝的取值范围．
【答案】（Ⅰ）1；（Ⅱ）﹣4＜y＜﹣2．
【解析】
（Ⅰ）首先把y＝2代入直线的解析式，求得交点坐标，然后利用待定系数法求得反比例函数的解析式，最后把x＝4代入求解；
（Ⅱ）首先求得当x＝﹣2和x＝﹣1时y的值，然后根据反比例函数的性质求解．
解：（Ⅰ）在y＝x中，当y＝2时，x＝2，则交点坐标是（2，2），
把（2，2）代入y＝
，得：k＝4，
所以反比例函数的解析式为y＝
，
当x＝4，y＝
＝1；
（Ⅱ）当x＝﹣2时，y＝
＝﹣2；
当x＝﹣1时，y＝
＝﹣4，
则当﹣2＜x＜﹣1时，反比例函数y＝的范围是：﹣4＜y＜﹣2．
练习册系列答案
相关题目
