题目内容
如图在Rt△AOB 中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程![]() 两根,且OA<AB.
两根,且OA<AB.
(1)求直线AB的解析式;
(2)将△AOB沿垂直于x轴的线段CD折叠(点C在x轴上,且不与点B重合,点D在线段AB上),使点B落在x轴上,对应点为E,是否存在这样的点C,使得△AED为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由.
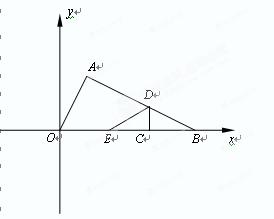

ⅱ)当Rt△AED以点E为直角顶点时,如图③,过点A作AF⊥x轴于F.
 OF=1.
OF=1.
∵∠AED=90°,∴∠AEO+∠DEC=90°.
∵∠DEC=∠DBC,∴∠AEO+∠DBC=90°.
又∠AOE+∠DBC=90°,∴∠AOE=∠AEO.
∴△AOE是等腰三角形,∴OE=2OF=2,∴BE=3.
∴EC=![]() ,∴OC=OE+E
,∴OC=OE+E![]() C=2+
C=2+![]() =
=![]() .
.
∴C2(![]() ,0).
,0).
综上所述,存在这样的点C,使得△AED为直角三角形,点C的坐标为:
C1(![]() ,0)和C2(
,0)和C2(![]()
![]() ,0).………………12分
,0).………………12分

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
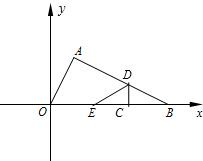 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为_________.
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为_________.
 两根,且OA<AB.
两根,且OA<AB.