题目内容
13.当方程x2+2(a+1)x+a2+4a-5=0有实数根时,a的正整数解为3,2,1.分析 利用根的判别式计算得出△,进一步根据a的取值范围得出a的正整数解即可.
解答 解:∵方程x2+2(a+1)x+a2+4a-5=0有实数根,
∴△=[2(a+1)]2-4(a2+4a-5)=4a2+8a+4-4a2-16a+20=-8a+24≥0,
解得:a≤3,
∴a的正整数解为3,2,1.
故答案为:3,2,1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
13.解方程$\frac{3x-5}{2}-2=\frac{7-x}{3}$时,去分母正确的是( )
| A. | 3x-15-2=14-2x | B. | 9x-15-6=14-x | C. | 3(3x-5)-12=2(7-x) | D. | 3(3x-5)-12=7-x |
1.数轴上表示-5$\frac{1}{3}$的点在( )
| A. | -5与-6之间 | B. | -6与-7之间 | C. | 5与6之间 | D. | 6与7之间 |
2.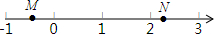 如图,M、N两点在数轴上表示的数分别是m,n,下列式子中成立的是( )
如图,M、N两点在数轴上表示的数分别是m,n,下列式子中成立的是( )
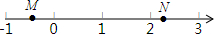 如图,M、N两点在数轴上表示的数分别是m,n,下列式子中成立的是( )
如图,M、N两点在数轴上表示的数分别是m,n,下列式子中成立的是( )| A. | m+n<0 | B. | -m<-n | C. | 2+m>2+n | D. | |m|-|n|>0 |
 由n个相同的小正方体组成的几何体,从正面和上面看到的几何体的形状如图所示,则n的最小值是12.
由n个相同的小正方体组成的几何体,从正面和上面看到的几何体的形状如图所示,则n的最小值是12.