题目内容
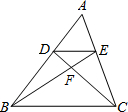如图，△ABC中，DE∥BC，CD、BE交于点F，如果EF：BF=2；5，那么AE：EC=________．
2：3
分析：由DE∥BC，即可得△ADE∽△ABC，△DEF∽△CBF，又由相似三角形的对应边成比例，即可得AE：AC=DE：BC=EF：BF=2：5，即可求得AE：EC的值．
解答：∵DE∥BC，
∴△ADE∽△ABC，△DEF∽△CBF，
∴AE：AC=DE：BC，DE：BC=EF：BF=2：5，
∴AE：AC=2：5，
∴AE：EC=2：3．
故答案为：2：3．
点评：此题考查了相似三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用，注意比例线段的对应关系．
分析：由DE∥BC，即可得△ADE∽△ABC，△DEF∽△CBF，又由相似三角形的对应边成比例，即可得AE：AC=DE：BC=EF：BF=2：5，即可求得AE：EC的值．
解答：∵DE∥BC，
∴△ADE∽△ABC，△DEF∽△CBF，
∴AE：AC=DE：BC，DE：BC=EF：BF=2：5，
∴AE：AC=2：5，
∴AE：EC=2：3．
故答案为：2：3．
点评：此题考查了相似三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用，注意比例线段的对应关系．
练习册系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．