题目内容
如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )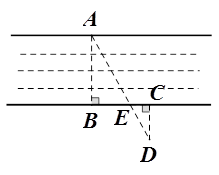
| A.30m | B.60m | C.20m | D.40m |
D.
解析试题分析:因为AB⊥BC,DC⊥BC,所以AB∥CD,所以ΔABE∽ΔDCE,所以有AB:CD=BE:CE,又BE=20m,CE=10m,CD=20m,所以AB=40m.故选D.
考点:1、相似三角形的判定;2、相似三角形的性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
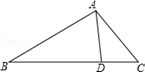
如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A.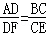 | B. | C. | D.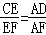 |
如图,在△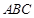 中,点
中,点 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且 ∥
∥ ,若
,若 ,
,  ,
, 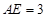 ,则
,则 的长为( )
的长为( )
| A.3 | B.6 | C.9 | D.12 |
若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
| A. 1:2 | B. 1:4 | C. 1:5 | D.1:16 |
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=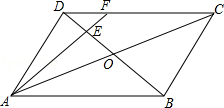
| A.1:4 | B.1:3 | C.2:3 | D.1:2 |
 中,
中, ,
, ,
, 的平分线交
的平分线交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,
, ,垂足为
,垂足为 .若
.若 ,则△
,则△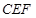 的面积是( )
的面积是( )



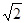




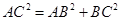 B.
B.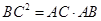 C.
C.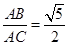 D.
D.
 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 都是
都是 方格纸(每个小方格均为正方形)中的格点,为使△
方格纸(每个小方格均为正方形)中的格点,为使△ ∽△
∽△ ,则点
,则点 应是
应是 、
、