题目内容
如图,在 中,
中, ,
, ,
, 的平分线交
的平分线交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,
, ,垂足为
,垂足为 .若
.若 ,则△
,则△ 的面积是( )
的面积是( )
A. | B. | C. | D.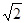 |
A.
解析试题分析:∵AE平分∠BAD,
∴∠DAE=∠BAE;
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BEA=∠DAE=∠BAE,
∴AB=BE=6,
∵BG⊥AE,垂足为G,
∴AE=2AG.
在Rt△ABG中,∵∠AGB=90°,AB=6,BG=4 ,
,
∴AG= =2,
=2,
∴AE=2AG=4;
∴S△ABE= AE•BG=
AE•BG= ×4×4
×4×4 =8
=8 .
.
∵BE=6,BC=AD=9,
∴CE=BC﹣BE=9﹣6=3,
∴BE:CE=6:3=2:1.
∵AB∥FC,
∴△ABE∽△FCE,
∴S△ABE:S△CEF=(BE:CE)2=4:1,
则S△CEF= S△ABE=2
S△ABE=2 .
.
故选A.
考点:1.相似三角形的判定与性质,2.平行四边形的性质.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
如图,一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得此时影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
| A.3米 | B.4.5米 | C.6米 | D.8米 |
如图,在平行四边形ABCD中,AC与BD交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF∶FC=
| A.1∶4 | B.1∶3 | C.2∶3 | D.1∶2 |
下列多边形一定相似的为( )
| A.两个三角形 | B.两个四边形 | C.两个正方形 | D.两个平行四边形 |
若△ABC∽△A′B′C′,∠A=40°,∠B=60°,则∠C′等于 ( )
| A.20°; | B.40°; | C.60°; | D.80°. |
如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )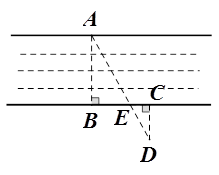
| A.30m | B.60m | C.20m | D.40m |
如图,在△ 中,
中, 为
为 边上一点,∠
边上一点,∠ ∠
∠ ,
, ,
, ,则
,则 的长为( )
的长为( )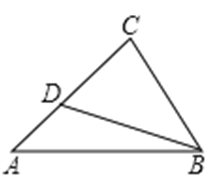
| A.1 | B.4 | C.3 | D.2 |
在比例尺 的地图上,量得两地的距离是
的地图上,量得两地的距离是 ,则这两地的实际距离是( )
,则这两地的实际距离是( )
A. | B. | C. | D. |

 B.
B. C.
C. D.
D.