题目内容
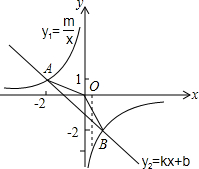 如图,已知A(-2,1)、B(a,-2)是反比例函数y1=
如图,已知A(-2,1)、B(a,-2)是反比例函数y1= 的图象与一次函数y2=kx+b的图象的两个交点.
的图象与一次函数y2=kx+b的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)△AOB的面积是______;
(3)观察图象可知:当y1<y2时,x的取值范围是______.
 解:(1)①将A(-2,1)代入y1=
解:(1)①将A(-2,1)代入y1= ,可得
,可得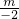 =1,
=1,解得m=-2,
∴y1=-
 ,
,②当y=-2时,x=1,
∴B(1,-2),
又将A(-2,1)、B(1,-2)代入y2=kx+b可得:
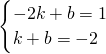 ,
,解得
 ,
,∴y2=-x-1;
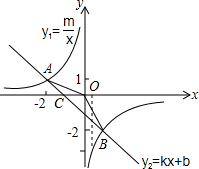
(2)令y2=0可得:-x-1=0,
∴x=-1,
∴C(-1,0),
S△AOB=S△AOC+S△BOC=
 ×1×1+
×1×1+ ×1×2=
×1×2= ,
,故答案为:
 ;
;(3)根据图象可得:当0<x<1或x<-2时,y1<y2.
故答案为:0<x<1或x<-2.
分析:(1)把A(-2,1)、B(a,-2)分别代入一次函数y=kx+b和反比例函数y=
 ,运用待定系数法分别求其解析式;
,运用待定系数法分别求其解析式;(2)把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算;
(3)看在交点的哪侧,对于相同的自变量,一次函数大于或等于反比例函数的函数值.
点评:此题主要考查了用待定系数法确定反比例函数的比例系数k,求出函数解析式;要能够熟练借助直线和y轴的交点运用分割法求得不规则图形的面积.同时间接考查函数的增减性来解不等式.

练习册系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=