题目内容
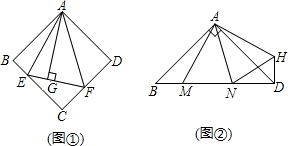
如图，若S△ABD：S△ACD=AB：AC，求证：AD平分∠BAC．分析：过D作DM⊥AB于M，DN⊥AC于N，根据三角形的面积求出DM=DN，再根据到角的两边距离相等的点在角的平分线上证明即可．
解答：证明
：如图，过D作DM⊥AB于M，DN⊥AC于N，
则S△ABD=
AB•DM，S△ACD=
AC•DN，
∵S△ABD：S△ACD=AB：AC，
∴DM=DN，
∴AD平分∠BAC．
：如图，过D作DM⊥AB于M，DN⊥AC于N，则S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABD：S△ACD=AB：AC，
∴DM=DN，
∴AD平分∠BAC．
点评：本题考查了到角的两边距离相等的点在角的平分线上，三角形的面积，熟记性质并作出辅助线是解题的关键．
练习册系列答案
相关题目
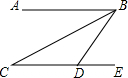（2007•海淀区二模）如图，BC平分∠ABD，AB∥CD，点E在CD的延长线上．若∠C=28°，则∠BDE的度数为（ ）
的形式写)
如图，若S△ABD：S△ACD=AB：AC，求证：AD平分∠BAC．