题目内容
正五边形ABCDE中,已知△ABC面积为1,则这正五边形面积是
- A.
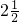
- B.

- C.

- D.

D
分析:由正五边形ABCDE中,已知△ABC面积为1,得出S△BCD=S△CDE=S△DEA=S△EAB=S△ACB=S△ACF=1.△AEF的边AF与△DEF的边DF上的高相等,及△DEF∽△ACF,求出S△AEF,然后即可求出五边形ABCDE的面积.
解答: 解:∵正五边形ABCDE中,已知△ABC面积为1,
解:∵正五边形ABCDE中,已知△ABC面积为1,
∴S△BCD=S△CDE=S△DEA=S△EAB=S△ACB=S△ACF=1.
设S△AEF=x,则S△DEF=1-x,
∵△AEF的边AF与△DEF的边DF上的高相等,
∴ .
.
∵△DEF∽△ACF,
∴ .
.
整理解得 .
.
故SABCDE=3S△ABC+S△AEF= .
.
故选D.
点评:本题考查了正多边形的计算,解题时还用到了图形的面积及相似三角形的判定和性质的知识.
分析:由正五边形ABCDE中,已知△ABC面积为1,得出S△BCD=S△CDE=S△DEA=S△EAB=S△ACB=S△ACF=1.△AEF的边AF与△DEF的边DF上的高相等,及△DEF∽△ACF,求出S△AEF,然后即可求出五边形ABCDE的面积.
解答:
 解:∵正五边形ABCDE中,已知△ABC面积为1,
解:∵正五边形ABCDE中,已知△ABC面积为1,∴S△BCD=S△CDE=S△DEA=S△EAB=S△ACB=S△ACF=1.
设S△AEF=x,则S△DEF=1-x,
∵△AEF的边AF与△DEF的边DF上的高相等,
∴
 .
.∵△DEF∽△ACF,
∴
 .
.整理解得
 .
.故SABCDE=3S△ABC+S△AEF=
 .
.故选D.
点评:本题考查了正多边形的计算,解题时还用到了图形的面积及相似三角形的判定和性质的知识.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
正五边形ABCDE中,已知△ABC面积为1,则这正五边形面积是( )
A、2
| ||||
B、3
| ||||
C、
| ||||
D、
|
 25、如图,在正五边形ABCDE中,连接对角线AC,AD和CE,AD交CE于F.
25、如图,在正五边形ABCDE中,连接对角线AC,AD和CE,AD交CE于F.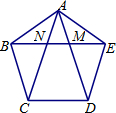 7、如图,在正五边形ABCDE中,对角线AD,AC与EB分别相交于点M,N.下列结论错误的是( )
7、如图,在正五边形ABCDE中,对角线AD,AC与EB分别相交于点M,N.下列结论错误的是( )
 如图,圆内接正五边形ABCDE中,∠ADB=( )
如图,圆内接正五边形ABCDE中,∠ADB=( )