Question

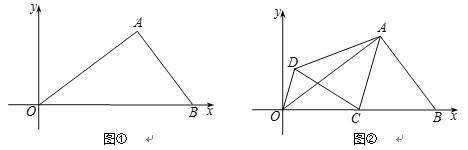
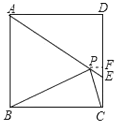
【题目】如图，在正方形中，，把边绕点逆时针旋转30°得到线段，连接并延长交于点，连接，则三角形的面积为__________．

Answer 1

【答案】

【解析】

根据旋转的性质得BP＝BC＝AB＝AD＝，∠PBC＝30°，推出△ABP是等边三角形，得到∠BAP＝60°，AP＝AB＝，解直角三角形求出AE和DE，过P作PF⊥CD于F，求出PF即可解决问题．

解：∵四边形ABCD是正方形，

∴∠ABC＝90°，

∵把边BC绕点B逆时针旋转30°得到线段BP，

∴BP＝BC＝AB＝AD＝，∠PBC＝30°，

∴∠ABP＝60°，

∴△ABP是等边三角形，

∴∠BAP＝60°，AP＝AB＝，

∴∠DAE＝30°，

∴AE＝，DE＝4，

∴CE＝，PE＝8，

过P作PF⊥CD于F，则∠EPF＝30°，

∴PF＝PE·cos30°＝，

∴三角形PCE的面积＝CEPF＝，

故答案为：．