Question

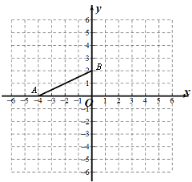
【题目】已知抛物线与轴只有一个交点，且与轴交于点，如图，设它的顶点为B．

（1）求的值；

（2）过A作x轴的平行线，交抛物线于点C，求证：△ABC是等腰直角三角形；

（3）将此抛物线向下平移4个单位后，得到抛物线，且与x轴的左半轴交于E点，与y轴交于F点，如图．请在抛物线上求点P，使得△是以EF为直角边的直角三角形？

Answer 1

【答案】（1）m = 2；（2）证明见解析；（3）满足条件的P点的坐标为（， ）或（， ）．

【解析】试题分析：（1）根据抛物线与x轴只有一个交点可知△的值为0，由此得到一个关于m的一元一次方程，解此方程可得m的值；

（2）根据抛物线的解析式求出顶点坐标，根据A点在y轴上求出A点坐标，再求C点坐标，根据三个点的坐标得出△ABC为等腰直角三角形；

（3）根据抛物线解析式求出E、F的坐标，然后分别讨论以E为直角顶点和以F为直角顶点P的坐标．

试题解析：（1）∵抛物线y=x2-2x+m-1与x轴只有一个交点，

∴△=（-2）2-4×1×（m-1）=0，

解得，m=2；

（2）由（1）知抛物线的解析式为y=x2-2x+1=（x-1）2，易得顶点B（1，0），

当x=0时，y=1，得A（0，1）．

由1=x2-2x+1，解得，x=0（舍）或x=2，所以C点坐标为：（2，1）．

过C作x轴的垂线，垂足为D，则CD=1，BD=xD-xB=1．

∴在Rt△CDB中，∠CBD=45°，BC=．

同理，在Rt△AOB中，AO=OB=1，于是∠ABO=45°，AB=．

∴∠ABC=180°-∠CBD-∠ABO=90°，AB=BC，

因此△ABC是等腰直角三角形；

（3）由题知，抛物线C′的解析式为y=x2-2x-3，

当x=0时，y=-3；

当y=0时，x=-1或x=3，

∴E（-1，0），F（0，-3），即OE=1，OF=3．

第一种情况：若以E点为直角顶点，设此时满足条件的点为P1（x1，y1），作P1M⊥x轴于M．

∵∠P1EM+∠OEF=∠EFO+∠OEF=90°，

∴∠P1EM=∠EFO，得Rt△EFO∽Rt△P1EM，

则，即EM=3P1M．

∵EM=x1+1，P1M=y1，

∴x1+1=3y1①

由于P1（x1，y1）在抛物线C′上，

则有3（x12-2x1-3）=x1+1，

整理得，3x12-7x1-10=0，解得，

x1＝，或x2=-1（舍去）

把x1＝代入①中可解得，

y1=．

∴P1（， ）．

第二种情况：若以F点为直角顶点，设此时满足条件的点为P2（x2，y2），作P2N⊥y轴于N．

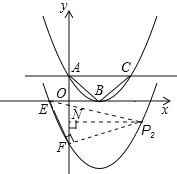
同第一种情况，易知Rt△EFO∽Rt△FP2N，

得，即P2N=3FN．

∵P2N=x2，FN=3+y2，

∴x2=3（3+y2）②

由于P2（x2，y2）在抛物线C′上，

则有x2=3（3+x22-2x2-3），

整理得3x22-7x2=0，解得x2=0（舍）或x2＝．

把x2＝代入②中可解得，

y2＝．

∴P2（，）．

综上所述，满足条件的P点的坐标为：（， ）或（，）.