题目内容
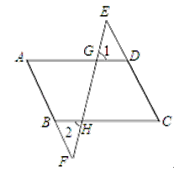
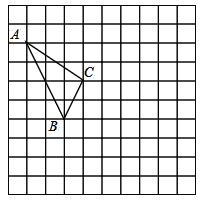
【题目】如图,抛物线y=![]() x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣
x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣![]() x﹣
x﹣![]() 交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
(1)求抛物线的解析式;
(2)当点P在直线L下方时,过点P作PN∥y轴交L于点N,求PN的最大值.
(3)当点P在直线L下方时,过点P作PM∥x轴交L于点M,求PM的最大值.

【答案】(1)抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;(2)PN的最大值是
x﹣2;(2)PN的最大值是![]() ;(3)PM的最大值是
;(3)PM的最大值是![]() .
.
【解析】试题分析:(1)把B(3,0),C(0,-2)代入y=![]() x2+bx+c解方程组即可得到结论;
x2+bx+c解方程组即可得到结论;
(2)设P(m, ![]() m2-
m2-![]() m-2),得到N(m,-
m-2),得到N(m,-![]() m-
m-![]() ),根据二次函数的性质即可得到结论;
),根据二次函数的性质即可得到结论;
(3)设P(m, ![]() m2-
m2-![]() m-2),得到M(-m2+2m+2,
m-2),得到M(-m2+2m+2, ![]() m2-
m2-![]() m-2),根据二次函数的性质即可得到结论.
m-2),根据二次函数的性质即可得到结论.
试题解析:(1)把B(3,0),C(0,﹣2)代入y=![]() x2+bx+c,
x2+bx+c,
得: 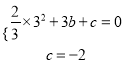 ,∴
,∴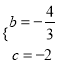 ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)设P(m, ![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
∵PN∥y轴,N在直线AD上,
∴N(m,﹣ ![]() m﹣
m﹣![]() ),
),
∴PN=﹣![]() m﹣
m﹣![]() ﹣
﹣![]() m2+
m2+![]() m+2=﹣
m+2=﹣![]() m2+
m2+![]() m+
m+![]() ,
,
∴当m=![]() 时,PN的最大值是
时,PN的最大值是![]() ;
;
(3)设P(m, ![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
∵PM∥x轴,M在直线AD上,M与P纵坐标相同,
把y=![]() m2﹣
m2﹣![]() m﹣2,代入y=﹣
m﹣2,代入y=﹣![]() x﹣
x﹣![]() 中,得x=﹣m2+2m+2,
中,得x=﹣m2+2m+2,
∴M(﹣m2+2m+2, ![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
∴PM=﹣m2+2m+2 -m= ﹣m2+m+2
∴当m=![]() 时,PM的最大值是
时,PM的最大值是![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目