题目内容
数学中,为了简便,记1+2+3+…+(n-1)+n=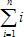 ,1×2×3×…×(n-1)×n=n!,那么,
,1×2×3×…×(n-1)×n=n!,那么,
+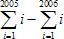 =( )
=( )
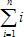 ,1×2×3×…×(n-1)×n=n!,那么,
,1×2×3×…×(n-1)×n=n!,那么,| 2006! |
| 2005! |
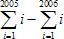 =( )
=( )| A、0 | B、1 |
| C、2005 | D、2006 |
分析:此题先用自定义变成常规式子,再按照运算顺序计算.
解答:解:
+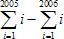
=
+(1+2+3+…+2005)-(1+2+3+…+2006)
=2006+[(1+2+3+…+2005)-(1+2+3+…+2006)]
=2006+(-2006)
=0
故选A.
| 2006! |
| 2005! |
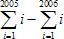
=
| 1×2×3×…×2006 |
| 1×2×3×…×2005 |
=2006+[(1+2+3+…+2005)-(1+2+3+…+2006)]
=2006+(-2006)
=0
故选A.
点评:运算中应用运算定律可使问题简单化.

练习册系列答案
相关题目
