Question

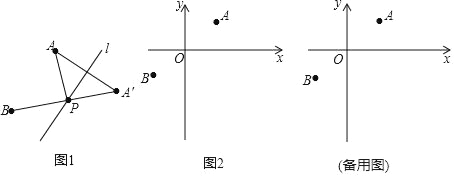
【题目】如图1，在平面直角坐标系中，直线经过点，与轴，轴分别交于，两点，点，

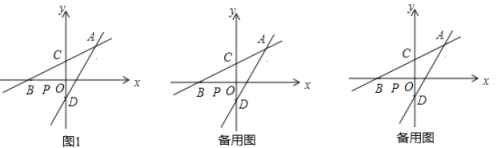
（1）求的值和直线的函数表达式；

（2）连结，当是等腰三角形时，求的值；

（3）若，点，分别在线段，线段上，当是等腰直角三角形且时，则的面积是______.

Answer 1

【答案】（1），直线AD的表达式为：（2）t的值为或或；（3）的面积是或．

【解析】

（1）将A点代入即可求得m的值， 根据D点设直线AD的一般式，将A点代入求得k的值即可；

（2）分以BC为底和以BC为腰（其中BC为腰又分为以B点为顶点和以C点为顶点分别讨论）两种情况讨论，画出相应的图形，根据图形分析即可得出t的值；

（3）分以M为直角顶点和以N为直角顶点，构造全等三角形，进行分析即可求出的面积．

解：（1）将代入中的得，解得，

因为，所以设直线AD的解析式为：，

将代入得，解得，所以；

（2）如下图，

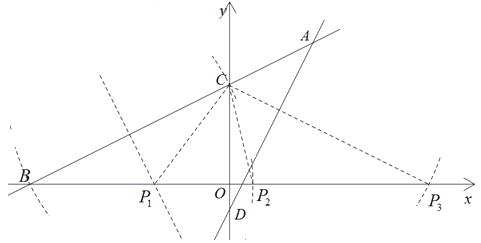
由直线可知,

当y=0时，，解得x=-8，所以,

①当等腰以BC为底时，P点在BC的垂直平分线与x轴交点处，

则此时，

即，解得；

②当等腰以BC为腰时，若B点为顶点，则以B点为圆心，BC为半径画弧，在B点右侧（因为）与x轴相交于，

∵,

∴，

若C点为顶点，则以C点为圆心，BC为半径画弧，与x正半轴交于处，

∴，即，

综上所述t的值为或或．

（3）①当是以M为直角顶点的等腰直角三角形，如下图，

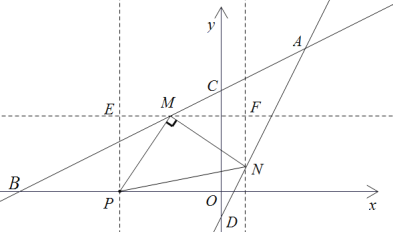
分别过P点和N点作x轴垂线与过M点作y轴的垂线相交于E，F,

则∵EP垂直x轴，FN垂直x轴，EF垂直y轴

∴∠PEF=∠EFN=90°，

∴∠EPM+∠EMP=90°，

∵∠PMN=90°，

∴∠FMN+∠EMP=90°，

∴∠EPM=∠FMN，

又∵PM=MN，

∴△PEM≌△MFN

∴设MF=EP=m，NF=ME=n，

∵P(-4,0),

∴，

分别将M和N代入和中

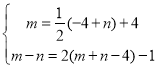解得，

∴，;

当是以N为直角顶点的等腰直角三角形，如下图，

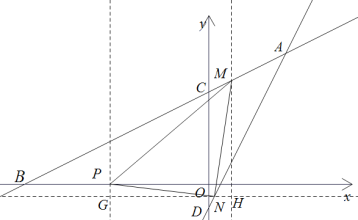
分别过P点和M点作x轴垂线与过N点作y轴的垂线相交于G，H,

与本小题①同理可证△NPG≌△MNH

设，

则

分别将M和N代入和中，

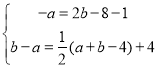，解得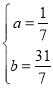

所以，

故的面积是或．