题目内容
8．一个等腰三角形的两条边长为3，7，那么它的周长是17．分析 题目给出等腰三角形有两条边长为7和3，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．
解答 解：当腰为7时，周长=7+7+3=17；
当腰长为3时，根据三角形三边关系可知此情况不成立；
根据三角形三边关系可知：等腰三角形的腰长只能为7，这个三角形的周长是17，
故答案为：17．
点评 本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
练习册系列答案
相关题目
18．设甲数为a，乙数为b，甲乙两数的平方和与甲乙两数积的商的代数式是（ ）
| A． | $\frac{{a}^{2}+{b}^{2}}{ab}$ | B． | （a+b）2ab | C． | （a2+b2）$\frac{a}{b}$ | D． | $\frac{（a+b）^{2}}{ab}$ |
16．已知三角形三边长分别为3，x，14，若x为正整数，则这样的三角形个数为（ ）
| A． | 2 | B． | 3 | C． | 5 | D． | 13 |
20．若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根，则k的取值范围是（ ）
| A． | k＞-1 | B． | k＞-1且k≠0 | C． | k＜1 | D． | k＜1且k≠0 |
17．下列说法中，不正确的是（ ）
| A． | 任意一个负实数的绝对值都是它的相反数 | |
| B． | 任意一个实数都有相反数 | |
| C． | 任意一个实数都有倒数 | |
| D． | 任意一个实数都可以在数轴上找到一点与其对应 |
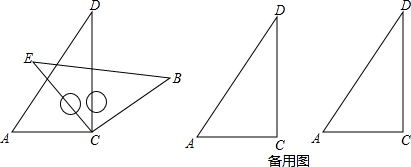
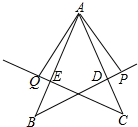已知，如图，AB=AC，AD=AE，AP⊥BD，AQ⊥CE，垂足分别为P、Q，求证：AP=AQ．