题目内容
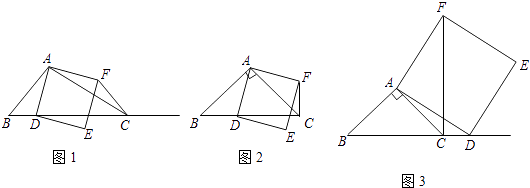
【题目】如图所示，△ABC中，∠ACB=90°，AC=6cm，BC =8cm.点P从A点出发,沿
路径向终点B运动，点Q从B点出发,沿
路径向终点A运动.点P 和Q分别
和
的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过点P和Q作PE⊥l于E，QF⊥l于F.则点P运动多少秒时，△PEC和△CFQ全等？请说明理由.
【答案】1秒或3.5秒或12秒
【解析】
因为
和
全等，所以
，有三种情况：
在
上，
在
上②
,都在上，此时,重合③当到达
点(和点重合)，在上时，此时点停止运动.根据这三种情况讨论.
设运动时间为
秒时，
和
全等，
∵和全等，
∴，
有三种情况：
如图1所示，在上，在上，
，
，
∴
，
∴
.
（2）如图2所示，,都在上，此时,重合，，
，
∴
，
∴
.
（3）如图3所示，当到达点(和点重合)，在上时，此时点停止运动，
∵，
，
，
∴
，
∴
.
∵
，
∴符合题意.
答：点运动1秒或3.5秒或12秒时，和全等. 
练习册系列答案
相关题目
