题目内容
已知抛物线y=
经过点A（4，0），点C（3，-3），请在抛物线的对称轴上确定一点D，使得AD+CD的值最小，则D点的坐标为________．
D（2，-2）
分析：根据两点之间线段最短、抛物线的对称性找到点D；然后设过点A′、D、C的直线方程是y=kx（k≠0），通过待定系数法求得该直线的解析式；最后由正比例函数图象上点的坐标特征求得点D的坐标即可．
解答：
解：∵抛物线y=经过点A（4，0），
∴0=
×42+4b，
解得，b=-2；
∴该抛物线的对称轴是：x=-
=2；
∴点A关于x=2对称的点是A′（0，0）；
∴AD=A′D，AD+DC=A′D+DC；
∵两点之间线段最短，∴要使得AD+CD的值最小，只需点A′、D、C共线；
连接A′C交对称轴x=2于点D，点D即为所求；
故设过点A′C的直线是y=kx（k≠0），点D（2，m），
∴-3=3k，
解得k=-1，
∴点D在直线y=-x上，
∴m=-2，
即点D的坐标是（2，-2）；
故答案是：D（2，-2）．
点评：本题考查了二次函数综合题．其中涉及到了待定系数法求二次函数解析式、二次函数的对称轴以及二次函数图象的对称性等有关于二次函数的知识点．
分析：根据两点之间线段最短、抛物线的对称性找到点D；然后设过点A′、D、C的直线方程是y=kx（k≠0），通过待定系数法求得该直线的解析式；最后由正比例函数图象上点的坐标特征求得点D的坐标即可．
解答：
解：∵抛物线y=经过点A（4，0），∴0=
×42+4b，解得，b=-2；
∴该抛物线的对称轴是：x=-
=2；∴点A关于x=2对称的点是A′（0，0）；
∴AD=A′D，AD+DC=A′D+DC；
∵两点之间线段最短，∴要使得AD+CD的值最小，只需点A′、D、C共线；
连接A′C交对称轴x=2于点D，点D即为所求；
故设过点A′C的直线是y=kx（k≠0），点D（2，m），
∴-3=3k，
解得k=-1，
∴点D在直线y=-x上，
∴m=-2，
即点D的坐标是（2，-2）；
故答案是：D（2，-2）．
点评：本题考查了二次函数综合题．其中涉及到了待定系数法求二次函数解析式、二次函数的对称轴以及二次函数图象的对称性等有关于二次函数的知识点．
练习册系列答案
相关题目
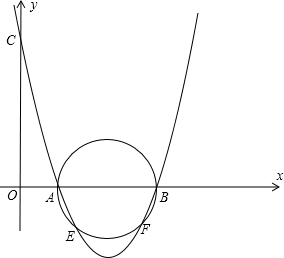已知抛物线经过点A（1，0）、B（3，0）、C（0，3），以AB为直径画圆．
如图，已知抛物线经过点A（-3，0），B（0，3），C（2，0）三点．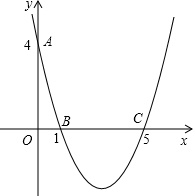
如图，在平面直角坐标系xoy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线对称轴l与x轴相交于点M．