题目内容
11.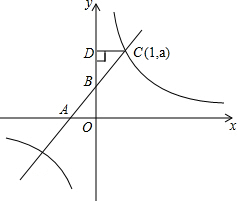 如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C(1,a),点E(b,-2)是直线与双曲线y=$\frac{m}{x}$的两个交点,过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.
如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C(1,a),点E(b,-2)是直线与双曲线y=$\frac{m}{x}$的两个交点,过点C作CD⊥y轴,垂足为D,且△BCD的面积为1.(1)求直线AB的解析式和点E坐标:
(2)根据图象直接写出不等式kx+2≤$\frac{m}{x}$的解集.
分析 (1)可先求得B点坐标,再结合△BCD的面积可求得a的值,可求得C点坐标,代入直线解析式可求得k的值,可求得直线AB解析式;再把E点坐标代入直线AB解析式可求得b,可求得E点坐标;
(2)把点C坐标代入双曲线解析式可求得m的值,不等式的解析集即为直线在双曲线下方时对应的x的范围,结合图象可求得其解集.
解答 解:(1)在y=kx+2中,令x=0可得y=2,
∴B点坐标为(0,2),
∵CD⊥y轴,且C(1,a),
∴D点坐标为(0,a),
∴OB=2,OD=a,CD=1,
∴S△BCD=$\frac{1}{2}$BD•CD=$\frac{1}{2}$×1×(a-2)=1,
∴a=4,
∴C点坐标为(1,4),
∵C点在直线AB上,
∴4=k+2,解得k=2,
∴直线AB解析式为y=2x+2,
∵E点在直线AB上,
∴-2=2b+2,解得b=-2,
∴E点坐标为(-2,-2);
(2)∵C在双曲线上,
∴m=4,
∴双曲线解析式为y=$\frac{4}{x}$,
∵不等式kx+2≤$\frac{m}{x}$的解集即为直线在双曲线下方对应的x的取值范围,
∴不等式的解集为x≤-2或x≥1.
点评 本题主要考查一次函数与反比例函数的交点,掌握两函数图象的交点坐标满足两函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.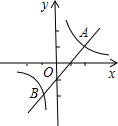 如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )
如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )
 如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )
如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )| A. | x>2 | B. | -1<x<0或x>2 | C. | -1<x<2 | D. | x<-1或x>2 |
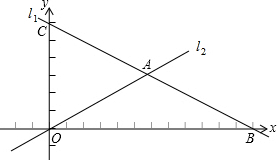 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.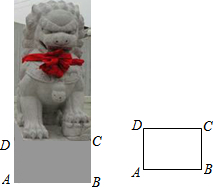 如图,李叔叔想要检测雕塑底座正面的AD和BC是否分别垂直于底边AB,但他随身只带了有刻度的卷尺.
如图,李叔叔想要检测雕塑底座正面的AD和BC是否分别垂直于底边AB,但他随身只带了有刻度的卷尺. 如图,直线y=-x+3与x轴,y轴分别交于点A、B两点,与y=$\frac{k}{x}$的图象交于C、D.CE⊥OA于E.若△BOD与△ACE的面积之和为5.
如图,直线y=-x+3与x轴,y轴分别交于点A、B两点,与y=$\frac{k}{x}$的图象交于C、D.CE⊥OA于E.若△BOD与△ACE的面积之和为5.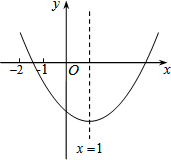 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论: 如图,已知AB=AC,DE=DF,求证:BE=CF.
如图,已知AB=AC,DE=DF,求证:BE=CF.