题目内容
问题背景
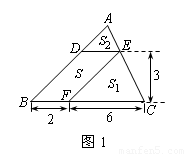
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:四边形DBFE的面积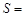 ,△EFC的面积
,△EFC的面积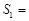 ,△ADE的面积
,△ADE的面积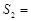 .
.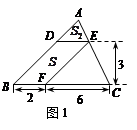
探究发现
(2)在(1)中,若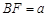 ,
, ,DE与BC间的距离为
,DE与BC间的距离为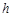 .请证明
.请证明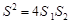 .
.
拓展迁移
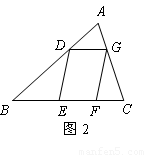
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.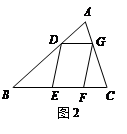
(1) ,
, ,
, (2)
(2)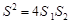 (3)18
(3)18
解析试题分析:(1) ,
, ,
, . 3分
. 3分
(2)证明:∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形, ,
, .
.
∴△ADE∽△EFC. 4分
∴ .
.
∵ ,
,
∴ . 5分
. 5分
∴ .
.
而 , ∴
, ∴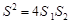 6分
6分
(3)解:过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形.
∴ ,
, ,
, .
.
∵四边形DEFG为平行四边形,
∴ . ∴
. ∴ .
.
∴ . ∴△DBE≌△GHF.
. ∴△DBE≌△GHF.
∴△GHC的面积为 . 8分
. 8分
由(2)得,□DBHG的面积为 . 9分
. 9分
∴△ABC的面积为 . 10分
. 10分
(说明:未利用(2)中的结论,但正确地求出了△ABC的面积,给2分)
考点:相似三角形
点评:本题属于对相似三角形,全等三角形等知识点的综合考察。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ▲ ,
▲ , ▲ ,
▲ , ▲ .
▲ . ,
, ,DE与BC间的距离为
,DE与BC间的距离为 .请证明
.请证明 .
.

 ,
, ,
, .
. ,
, ,DE与BC间的距离为
,DE与BC间的距离为 .请证明
.请证明 .
.
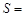 ▲
,
▲
,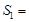 ▲ ,
▲ ,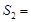 ▲ .
▲ .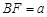 ,
,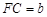 ,DE与BC间的距离为
,DE与BC间的距离为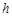 .请证明
.请证明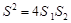 .
.

 ▲ ,
▲ , ,
, ,DE与BC间的距离为
,DE与BC间的距离为 .请证明S2=4S1 S2.
.请证明S2=4S1 S2.