题目内容
 一个长为10m的梯子斜靠在墙上,梯子底端距墙底6m.
一个长为10m的梯子斜靠在墙上,梯子底端距墙底6m.
(1)若梯子的底端水平向外滑动1m,梯子的顶端下滑多少米?
(2)如果梯子顶端向下滑动的距离等于底端向外滑动的距离,那么滑动的距离是多少米?
 解:(1)在△ABC中,∠ACB=90°,AB=10米,BC=6米,由勾股定理得AC=8米,
解:(1)在△ABC中,∠ACB=90°,AB=10米,BC=6米,由勾股定理得AC=8米,△A1BC1中,∠C=90°,A1B1=10米,B1C=7米,由勾股定理得A1C=
 米,
米,∴AB1=AC-B1C=(8-
 )米.
)米.答:它的顶端下滑动(8-
 )米.
)米.(2)设梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等为x,
根据题意,
10=
 解得,
解得,x=2米,
答:滑动的距离为2米.
分析:(1)已知AB,BC,在直角△ABC中即可计算AC,梯子底端水平向外滑动1m,即BC1=7米,A1B1=AB=10米,在直角△CA1B1中,根据勾股定理即可计算CA1,底端滑动的距离为CA-CA1;
(2)设这个相等的距离为x,根据勾股定理,列出方程,求解,得出x,
点评:本题考查的是对勾股定理在解直角三角形中的应用,要求熟练掌握.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 一个长为10m的梯子斜靠在墙上,梯子底端距墙底6m.
一个长为10m的梯子斜靠在墙上,梯子底端距墙底6m.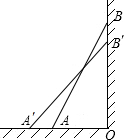 如图所示,一个长为10m的梯子AB靠在墙上,梯子的顶端B到墙根O的距离为8m,如果梯子的顶端B沿墙下滑1m,那么梯子的底端A向外移到A′,那么AA′( )
如图所示,一个长为10m的梯子AB靠在墙上,梯子的顶端B到墙根O的距离为8m,如果梯子的顶端B沿墙下滑1m,那么梯子的底端A向外移到A′,那么AA′( ) 一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.
一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m. 一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直离为8m.若梯子的顶端下滑2m后,低端将水平滑动( )m.
一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直离为8m.若梯子的顶端下滑2m后,低端将水平滑动( )m.