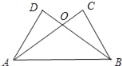
题目内容
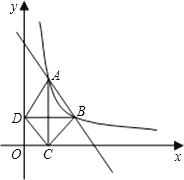
【题目】如图(1),在矩形DEFG中,DE=3,EG=6,在Rt△ABC中,∠ABC=90°,BC=3,AC=6,△ABC的一边BC和矩形的一边DG在同一直线上,点C和点D重合,Rt△ABC将从D以每秒1个单位的速度向DG方向匀速平移,当点C与点G重合时停止运动,设运动时间为t秒,解答下列问题:
(1)如图(2),当AC过点E时,求t的值;
(2)如图(3),当AB与DE重合时,AC与EF、EG分别交于点M、N,求CN的长;
(3)在整个运动过程中,设Rt△ABC与△EFG重叠部分面积为y,请求出y与t的函数关系式,并写出相应t的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)
【解析】分析:(1)当AC过点E时,△ABC∽△EDC,然后根据相似三角形的对应边成比例列比例方程可求出CD的值;
(2)由勾股定理求得DG=3![]() ,由sin∠EGD=
,由sin∠EGD=![]() 可求得∠EGD=30°,进而可求∠CNG=30°,根据等角对等边可知NC=CG,从而结论可求;
可求得∠EGD=30°,进而可求∠CNG=30°,根据等角对等边可知NC=CG,从而结论可求;
(3)由(1)可知,当x>![]() 时,△ABC与△EFG有重叠部分.分①当
时,△ABC与△EFG有重叠部分.分①当![]() <t≤3时,y=S△EMN,②当3<t≤3
<t≤3时,y=S△EMN,②当3<t≤3![]() 时,y=S△EMN﹣S△EPQ,两种情况求解.
时,y=S△EMN﹣S△EPQ,两种情况求解.
详解:(1)如图(2),当AC过点E时,
在Rt△ABC中,BC=3,AC=6,
∴BC所对锐角∠A=30°,
∴∠ACB=60°,
依题意可知∠ABC=∠EDC=90°,
∵∠ACB=∠ECD,
∴△ABC∽△EDC,
∴![]() ,即
,即![]() ,
,
∴CD=![]() ,
,
∴t=CD=![]() ;
;
(2)如图(3),∵∠EDG=90°,DE=3,EG=6,
∴DG=![]() =
=![]() =3
=3![]() ,
,
在Rt△EDG中,sin∠EGD=![]() =
=![]() =
=![]() ,
,
∴∠EGD=30°,
∵∠NCB=∠CNG+∠EGD,
∴∠CNG=∠NCB﹣∠EGD=60°﹣30°=30°,
∴∠CNG=∠EGD,
∴NC=CG=DG﹣BC=3![]() ﹣3;
﹣3;
(3)由(1)可知,当x>![]() 时,△ABC与△EFG有重叠部分.
时,△ABC与△EFG有重叠部分.
分两种情况:
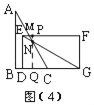
①当![]() <t≤3时,如图(4),△ABC与△EFG有重叠部分为△EMN,设AC与EF、EG分别交于点M、N,过点N作直线NP⊥EF于P,交DG于Q,
<t≤3时,如图(4),△ABC与△EFG有重叠部分为△EMN,设AC与EF、EG分别交于点M、N,过点N作直线NP⊥EF于P,交DG于Q,
则∠EPN=∠CQN=90°,
∵NC=CG,
∴NC=DG﹣DC=3![]() ﹣t,
﹣t,
在Rt△NQC中,NQ=sin∠NCQ×NC=sin60°×(3![]() ﹣t)=
﹣t)=![]() ,
,
∴PN=PQ﹣NQ=3﹣![]() =
=![]() ,
,
∵∠PMN=∠NCQ=60°,
∴sin∠PMN=![]() ,MN=
,MN=![]() =
=![]() ×
×![]() =t﹣
=t﹣![]() ,
,
在矩形DEFG中,EF∥DG,
∴∠MEN=∠CGN,
∵∠MNE=∠CNG,∠CNG=∠CGN,
∴∠EMN=∠MNE,
∴EM=MN,
∴EM=MN=t﹣![]() ,
,
∴y=S△EMN=![]() EMPN=
EMPN=![]() ×
×![]() ×
×![]() =
=![]() ﹣
﹣![]() ;
;
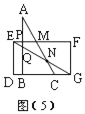
②当3<t≤3![]() 时,如图(5),△ABC与△EFG重叠部分为四边形PQNM,设AB与EF、EG分别交于点P、Q,AC与EF、EG分别交于点M、N,则∠EPQ=90°,
时,如图(5),△ABC与△EFG重叠部分为四边形PQNM,设AB与EF、EG分别交于点P、Q,AC与EF、EG分别交于点M、N,则∠EPQ=90°,
∵CG=3![]() ﹣t,
﹣t,
∴S△EMN=![]() ﹣
﹣![]() t+
t+![]() ,
,
∵EP=DB=t﹣3,∠PEQ=30°,
∴在Rt△EPQ中,PQ=tan∠PEQ×EP=tan30°×(t﹣3)=![]() ,
,
∴S△EPQ=![]() EPPQ=
EPPQ=![]() (t﹣3)×
(t﹣3)×![]() =
=![]() ,
,
∴y=S△EMN﹣S△EPQ=(![]() ﹣
﹣![]() t+
t+![]() )﹣(
)﹣(![]() )=
)=![]() +(
+(![]() ﹣
﹣![]() )t﹣
)t﹣![]() ,
,
综上所述,y与t的函数关系式:y=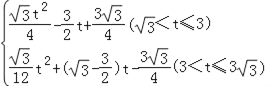 .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某同学在用描点法画二次函数![]() 的图象时,列出下面的表格:
的图象时,列出下面的表格:
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
根据表格提供的信息,有下列结论:
![]() 该抛物线的对称轴是直线
该抛物线的对称轴是直线![]() ;
;![]() ;
;![]() 该抛物线与y轴的交点坐标为
该抛物线与y轴的交点坐标为![]() ;
;![]() 若点
若点![]() 是该抛物线上一点,则
是该抛物线上一点,则![]() 其中错误的个数是
其中错误的个数是![]()
![]()
A. 4 B. 3 C. 2 D. 1
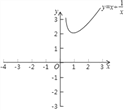
【题目】某数学兴趣小组对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 ,m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+![]() =3有 个实数根;
=3有 个实数根;
②若关于x的方程x+![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .